Wie Sie Ihre Planung und Vorhersage mit etwas Mathematik und KI verbessern können - Teil 1

Planungsirrtum

Planning Fallacy ist ein Begriff, der von Daniel Kahneman und Amos Tversky vorgeschlagen wurde. 1994 baten sie 37 Psychologiestudenten zu schätzen, wie lange sie für die Fertigstellung ihrer Doktorarbeit benötigen würden. Die durchschnittliche Schätzung lag bei 34 Tagen. Ihre "optimistischen" Schätzungen lagen bei 27 Tagen und ihre "pessimistischen" bei 49 Tagen. Tatsächlich benötigten sie für ihre Dissertation rund 56 Tage und nur 30% von ihnen hielten sich an ihre eigene Schätzung. [i]

Später, im Jahr 2004, baten Magne Jørgensen und Kjetil Moløkken 12 Softwareentwickler, 90%ige Schätzungen für 30 bereits abgeschlossene Aufgaben abzugeben. Diese Entwickler hatten Zugang zu einer kleinen Wissensdatenbank und wurden nach jeder Schätzung über den tatsächlichen Aufwand informiert. In diesem Experiment erhielten Jørgensen und Moløkken 360 Schätzungen, und obwohl "90% Zuversicht" herrschte, enthielten die Fachleute durchschnittlich 64% des tatsächlichen Aufwands für die ersten 10 Aufgaben, 70% für die nächsten 10 und 81% für die letzten 10 Aufgaben. Zusammenfassend lässt sich sagen, dass sie nie auch nur in die Nähe der angenommenen 90% Konfidenz kamen, obwohl sie nach jedem Versuch den richtigen Wert angegeben hatten. [ii]

Methoden zur Schätzung

Story Points sind ein "goldener Standard" in agilen Projekten. In der Tat sind sie sogar in diesen Projekten, die nicht wirklich agil sind, Standard. Und was noch interessanter ist: Sie finden im Scrum Guide kein einziges Wort über Story Points. Diese Punkte sind also gängige Praxis, eine Art Gewohnheit.

Sie bringen auch eine Menge Probleme mit sich:

• Schwer zu verstehen - Was schätzen wir wirklich? Aufwand? Wert? Zeit?
• Subjektivität
• Zeitaufwendig - Wer hat nicht an der Sitzung mit einer 1-stündigen Diskussion und einer geschätzten Aufgabe am Ende teilgenommen?
• Nicht klar für externe Stakeholder
• Und, was entscheidend ist, es kann Druck auf mehr Story Points im Sprint und eine höhere Geschwindigkeit ausgeübt werden - wenn wir hier bemerken, wie leicht das Team seine Schätzungen manipulieren kann, ist das ein fertiges Rezept für ein spätes Projekt.

Um die oben genannten Probleme zu vermeiden, können wir einige supereinfache Metriken aus Kanban-Frameworks verwenden. Sie erfordern nicht einmal Schätzungen des Teams:

• Vorlaufzeit
• Zykluszeit
• Unfertige Produkte
• Durchsatz

Langfristig gesehen sollte es in Ordnung sein, nur die Anzahl der Aufgaben zu berechnen, die das Team zu einem bestimmten Zeitpunkt erledigt hat, um die Zukunft vorherzusagen. Die Vereinfachung des Prozesses und die Verwendung alternativer Metriken kann eine Antwort auf den erwähnten Planungsirrtum sein, der in Teams so häufig vorkommt.

Aber vielleicht gibt es auch eine Möglichkeit, den gesamten Planungsprozess zu automatisieren, nicht nur die Schätzung? Kann Mathe hilfreich sein?

Monte-Carlo-Methode

Die Monte-Carlo-Methode oder das Monte-Carlo-Experiment geht davon aus, dass es bei komplexen Problemen schwierig sein kann, sie analytisch zu lösen. Stattdessen können wir nach dem Zufallsprinzip Werte auswählen, die für den Prozess repräsentativ sind, und dies mehrere tausend Mal wiederholen, um ein genaues Ergebnis zu erhalten.

Kreisfeld

Kann die Wahrscheinlichkeitsmethode wirklich echte Probleme lösen? Lassen Sie es uns versuchen. An wie viele Nachkommastellen π erinnern Sie sich? Es ist 3,14159... Und? Okay, vergessen Sie sie für eine Weile. Was können Sie tun, wenn Sie völlig vergessen haben, was π ist?

Zeichnen Sie ein Rechteck mit einem Kreis darin. Platzieren Sie dann zufällig Punkte innerhalb des Rechtecks. Einige von ihnen befinden sich natürlich auch innerhalb des Kreises.

Diese Simulation kann mit ChatGPT ausgeführt werden:

Eingabeaufforderung:

Zeichnen Sie ein Quadrat und schreiben Sie einen Kreis hinein. Platzieren Sie dann 100 Punkte zufällig innerhalb des Quadrats. Zählen Sie, wie viele davon gleichzeitig in den Kreis eingeschrieben sind.  

Für 100 Punkte haben wir 76 innerhalb des Kreises.

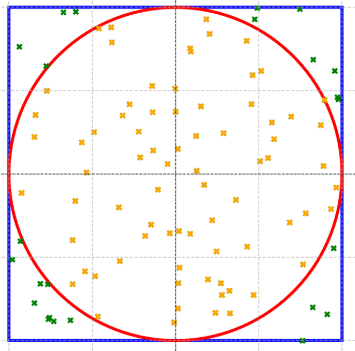
Um genauere Ergebnisse zu erhalten, versuchen Sie es mit mehreren Versuchen.

Eingabeaufforderung:

Wiederholen Sie das Experiment für 1000 Punkte.

Für 1000 Punkte haben wir 777 innerhalb des Kreises.

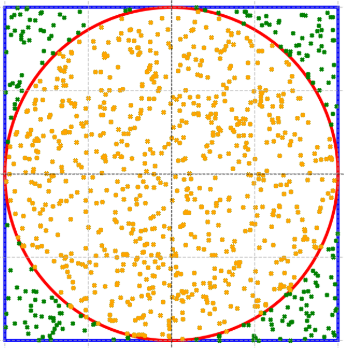
Mit der Monte-Carlo-Methode können wir also sagen, dass der Kreis innerhalb des Rechtecks etwa 0,78 des Rechteckfeldes abdeckt.

Lassen Sie uns ein wenig rechnen:

0,78 = Kreis_Feld / Rechteck_Feld
0,78 = π * r2  / (2r)2
0,78 = π / 4
π = 3,12

Ziemlich nah dran?

Deutsches Panzerproblem

Die Monte-Carlo-Methode wurde während des Zweiten Weltkriegs eingesetzt. Die Alliierten mussten abschätzen, wie viele Panzer der Rivale produzieren würde. Man nennt es das "Deutsche-Panzer-Problem". Jeder zerstörte deutsche Panzer hatte einige Elemente mit eindeutigen ID-Nummern. Diese Nummern wurden der Reihe nach vergeben. Die am besten zuordenbaren IDs wurden auf Getrieben gefunden, aber auch andere Teile wurden analysiert. Wir können davon ausgehen, dass die Panzer nach dem Zufallsprinzip zerstört wurden. Wenn wir also wissen, dass bereits zerstörte Panzer eine Identifikationsnummer haben:

[21, 25, 44, 56, 60, 72, 89, 134, 183, 249]

Wir können davon ausgehen, dass es sich um eine Zufallsstichprobe aus den produzierten Tanks handelt. Wie viele Panzer wurden demnach bereits produziert? Im nächsten Schritt können wir die durchschnittliche Differenz zwischen diesen ID-Nummern der Reihe nach berechnen. Die Unterschiede zwischen jedem aufeinanderfolgenden Zahlenpaar sind:

[4, 19, 12, 4, 12, 17, 45, 49, 66]
Durchschnittliche Differenz = 25,33.

Wir müssen nur diesen Wert zur höchsten Zahl aus der Sequenz addieren, um eine geschätzte Anzahl aller produzierten Tanks zu erhalten.

249 + 25 = 274

Wie genau war diese Berechnung damals? Nach Berechnungen der Alliierten waren im Februar 1944 etwa 270 deutsche Panzer auf dem Schlachtfeld. Den deutschen Aufzeichnungen zufolge waren es tatsächlich 276. Darüber hinaus ermöglichte diese Datenanalyse den Alliierten, die Funktionsweise der deutschen Panzerproduktion zu verstehen.[iii] Unter Berücksichtigung der aufgeblähten Propagandawerte brachte die Schätzung einen enormen Nutzen in der Konfrontation.

Monte-Carlo-Methode zur Schätzung

Wenn statistische Methoden für die Schätzung des Wertes von π und der Anzahl der Panzer auf dem Schlachtfeld funktionieren, sollten wir versuchen, sie in unserer täglichen Arbeit einzusetzen.

Die Zukunft ist nicht sicher und auch unsere Schätzungen und Vorhersagen darüber sind nicht sicher. Wir können auf der Grundlage unserer Geschwindigkeit und unserer Schätzungen berechnen, dass wir das Produkt zu einem bestimmten Zeitpunkt liefern werden. Es kann aber auch schon etwas früher oder später fertig sein. Wie groß ist also die Chance, dass es zum Stichtag fertig ist? Sind Sie fast sicher? Oder ist es nur fifty-fifty?

Es gibt eine Lösung, mit der Sie Ihrem Kunden mit absoluter Gewissheit sagen können, dass Ihr Projekt zu einem bestimmten Datum fertig sein wird. Um das zu berechnen, müssen wir etwas Mathematik anwenden.

Zunächst einmal benötigen Sie einige historische Daten. Sie können Story Points oder den Kanban-Ansatz verwenden, bei dem nur die Anzahl der in den vorangegangenen Timeboxen erledigten Aufgaben erfasst wird (dann brauchen Sie Ihr Product Backlog nicht wirklich zu schätzen).

In den vorangegangenen Sprints hat Ihr Team die Anzahl der Aufgaben oder Story Points geliefert:

[7, 8, 10, 15, 3, 4, 11, 12]

Wir können davon ausgehen, dass die Zukunft ähnlich sein wird. Führen Sie eine Simulation durch und weisen Sie dem zukünftigen Sprint diese Zahlen zufällig zu, solange Sie die erwartete Anzahl von Sprints zuweisen. In unserem Test möchten wir abschätzen, wie viele Story Points wir in den nächsten 10 Iterationen liefern werden. Ein einzelner Durchlauf ist nur eine einzige mögliche Vision der Zukunft, die auf Ihren Erfahrungen beruht. Sie können diese Simulationen mehrmals durchführen, um mehr mögliche Optionen zu sehen, und zwar mit jedem beliebigen Berechnungstool. Wir haben 15 Simulationen durchgeführt:

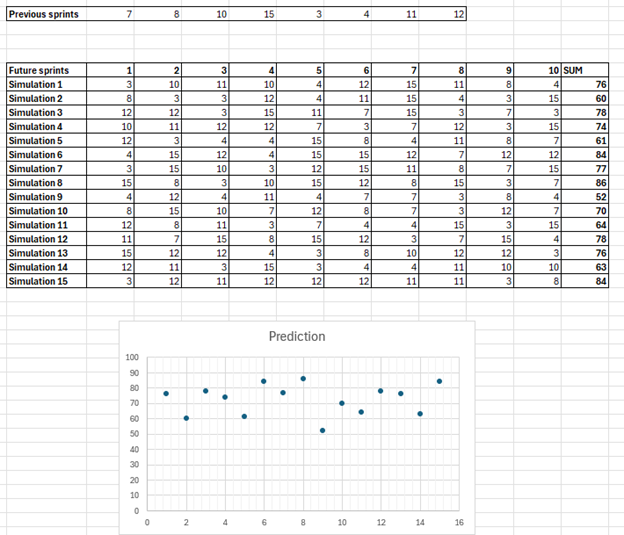
In der pessimistischsten Simulation wird das Team in den nächsten 10 Iterationen etwa 52 Aufgaben oder Story Points liefern, in der optimistischsten 86. Der Median liegt bei 76 - wir haben eine 50%ige Chance, in den nächsten 10 Iterationen nicht weniger als 76 zu liefern.

Um genauer zu sein, wiederholen Sie dieses Experiment 10000 Mal. Als Ergebnis erhalten Sie eine Gauß-Kurve, die eine mögliche Zukunft darstellt. Das nennt man Monte-Carlo-Simulation. Wenn Ihre erwartete Sicherheit sehr hoch ist, sagen wir 90%, müssen Sie 10% der optimistischsten Fälle ablehnen, um den Umfang oder die Frist zu berechnen.

Zusammenfassung

Die Schätzung zukünftiger Projekte muss kein Ratespiel sein. Selbst mit einer kleinen Stichprobe von Vergangenheitsdaten können Sie mögliche zukünftige Szenarien berechnen. Darüber hinaus können Sie sogar einen erwarteten Grad an Sicherheit festlegen und die Fristen für Ihr Projekt bekannt geben.

Im nächsten Artikel werden wir versuchen, einen KI-Assistenten zu bauen, der Ihnen hilft, Ihr Projekt schnell zu planen und detaillierte Fragen Ihrer Kunden in einer Sekunde zu beantworten.

 

Quellen:

[i] https://en.wikipedia.org/wiki/Planning_fallacy

[ii] https://link.springer.com/chapter/10.1007/978-3-540-24659-6_13

[iii] https://www.warhistoryonline.com/instant-articles/the-german-tank-problem.html