In a previous post, we talked about finding the partitions in a disconnected graph using Cascading. In reality, most graphs are actually fully connected, so only being able to partition already disconnected graphs is not very helpful. In this post, we’ll take a look at partitioning a connected graph based on some criterium for creating a partition boundary.
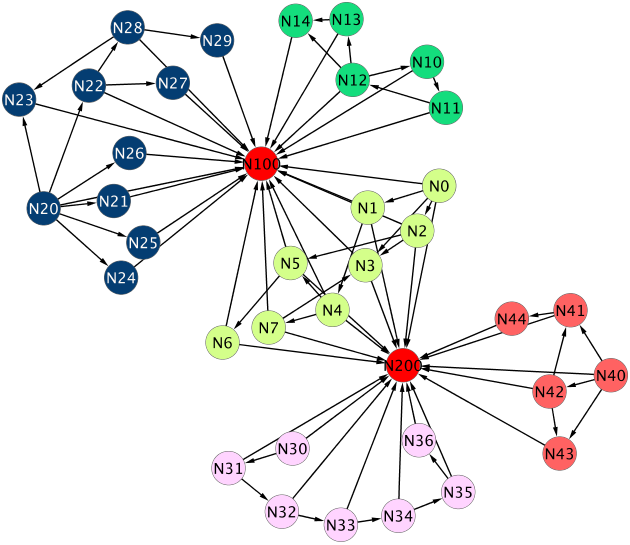
Let’s take the sample graph from previous post and make it a connected one. We’ll do this by adding two extra nodes that are connected to lots of other nodes in the graph. Like this:
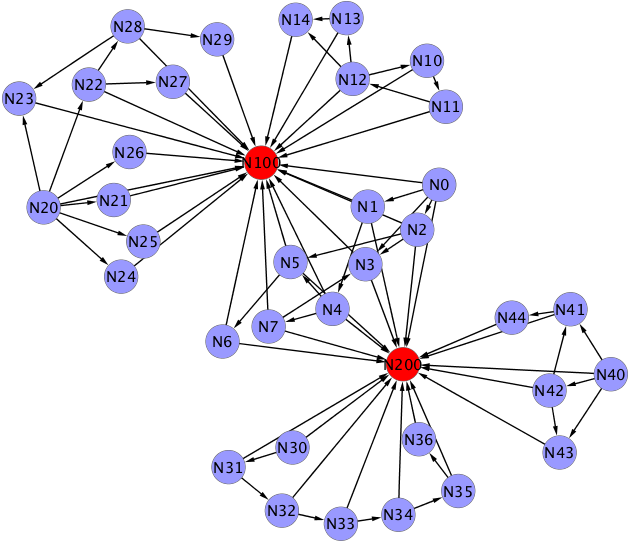
As you can see, the two highly connected nodes make the graph fully connected. If you would remove the highly connected (red) nodes, the graph would be the same, disconnected graph as the example from the previous post.
Partitioning criterium
In order to identify where the partitions should be created in the graph, we need some criterion to decide whether or not a particular edge should be followed when partitioning. In our example we will use the number of incoming connectiong of each node (indegree) to determine whether edges to that node will be included in a partition. So, we will count the number of incoming edges of each node and then mark te edges that point to nodes with a number of incoming edges greater than a certain threshold as edges not to follow. This will work, because the two nodes that connect everything together have a high number of incoming connections. This is of course not true for all graphs. In other cases you may want other partitioning criteria. If nodes in a graph represent geo locations, for example, you could use the distance between nodes to determine whether the edge between them should be followd. Any other function of two nodes that determines whether to follow the edge will work as well (as long as that function is symmetric). Also note that we mark edges to be excluded from following, not nodes.
Representation
Once we determine which edges to follow and which to leave out, we need some way of storing this information with the graph, such that the iterative job can make use of this information. One solution would be to store the indegree of each node as part of the data and evaluate for each edge whether we should follow it or not. This is however problematic. It would work for the edge counts, because the amount of data required for those is manageable. However, for more complex partitioning criteria, that need a lot of information about each node, the amount of carry on data just for partitioning would potentially be a lot. Instead, once we figured out which edges are interesting and which are not, we just store that fact along with the graph. We will do this in the form of a binary vector next to each adjacency list in the original representation. In the bit vector, a 1 means to include an edge and a 0 means to exclude an edge. For the graph above, with the two highly connected nodes, it would look like this:
3 0 200,2,1,100,3 0,1,1,0,1
4 1 200,100,4 0,0,1
5 2 5,3,200,100 1,1,0,0
3 3 200,100 0,0
7 4 100,5,7,200 0,1,1,0
6 5 100,200,6 0,0,1
6 6 100,200 0,0
7 7 100,3,200 0,1,0
11 10 100,11 0,1
12 11 12,100 1,0
14 12 13,14,100,10 1,1,0,1
14 13 14,100 1,0
14 14 100 0
26 20 22,21,26,25,100,24,23 1,1,1,1,0,1,1
21 21 100 0
28 22 27,28,100 1,1,0
23 23 100 0
24 24 100 0
25 25 100 0
26 26 100 0
27 27 100 0
29 28 23,100,29 1,0,1
29 29 100 0
31 30 31,200 1,0
32 31 32,200 1,0
33 32 33,200 1,0
34 33 200,34 0,1
35 34 200,35 0,1
36 35 200,36 0,1
36 36 200 0
43 40 41,200,42,43 1,0,1,1
44 41 44,200 1,0
43 42 200,43,41 0,1,1
43 43 200 0
44 44 200 0
Edge counting
In order to build the file as above, we need to calculate the indegree for each node in the graph and subsequently create adjacency lists together with the bit vectors. Each vector should have a 0 for positions on which the adjacency list has a target node with a high indegree (higher than a set threshold). To do this, we take the original graph in the edge list representation (see the previous post for an example) and follow these steps:
- Group by target node
- Count the number of occurrences of each target node (this count is the indegree for each node)
- Join that result back with the original set, such that the list is now: source
target count - Group by source node
- For every group, generate an adjacency list and bit vector
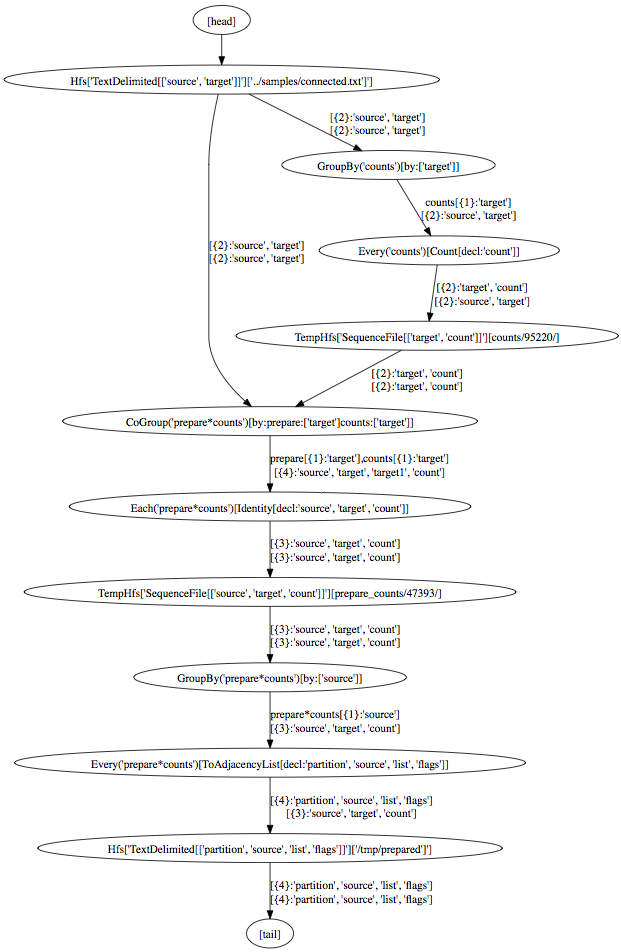
Cascading has the neat feature to write a .dot file representing a flow that you built. You can open these .dot files with a tool like GraphViz to turn them into a nice visual representation of your flow. What you see below is the flow for the job that creates the counts and subsequently the graph. The code for this job is here.
Skipping edges
Next, in the iterative part of our graph partitioning approach, we need to make sure that an edge that has a corresponding 0 in the bit vector, doesn’t tie two partitions together. In reality, this is very easy to achieve. Since we use sorting (using a secondary sort) to make sure that we always pick the largest possible partition, we just have to make sure that we sort the edges that we are not supposed to follow later than the ones we should follow. This means that, whenever we group edges, we just have to add one field to the sorting specification. Here’s the full code for this:
public class IterateWithFlagsJob { public int run(String input, String output, int maxIterations) { boolean done = false; int iterationCount = 0; while (!done) { Scheme sourceScheme = new TextDelimited(new Fields("partition", "source", "list", "flags"), "t"); Tap source = new Hfs(sourceScheme, currentIterationInputPath); Scheme sinkScheme = new TextDelimited(new Fields("partition", "source", "list", "flags"), "t"); Tap sink = new Hfs(sinkScheme, currentIterationOutputPath, SinkMode.REPLACE); //SNIPPED SOME BOILERPLATE... Pipe iteration = new Pipe("iteration"); //For each input record, create a record per node (step 3) iteration = new Each(iteration, new FanOut()); //GROUP BY node ORDER BY flag, partition DESCENDING iteration = new GroupBy( iteration, new Fields("node"), new Fields("flag", "partition"), //it works because of the flag! true); //For every group, create records with the largest partition iteration = new Every( iteration, new MaxPartitionToTuples(), Fields.RESULTS); //GROUP BY source node ORDER BY partition DESCENDING (step 4) iteration = new GroupBy( iteration, new Fields("source"), new Fields("flag", "partition"), //again, the flag! true); //For every group, re-create the adjacency list //with the largest partition //This step also updates the counter iteration = new Every( iteration, new MaxPartitionToAdjacencyList(), Fields.RESULTS); //SNIPPED SOME BOILERPLATE... flow.complete(); //Grab counter value? long updatedPartitions = flow.getFlowStats().getCounterValue( MaxPartitionToAdjacencyList.COUNTER_GROUP, MaxPartitionToAdjacencyList.PARTITIONS_UPDATES_COUNTER_NAME); //Are we done? done = updatedPartitions == 0 || iterationCount == maxIterations - 1; iterationCount++; } return 0; } private class MaxPartitionToAdjacencyListContext { int source; int partition = -1; ListInteger> targets; ListByte> flags; public MaxPartitionToAdjacencyListContext() { this.targets = new ArrayListInteger>(); this.flags = new ArrayListByte>(); } } @SuppressWarnings("serial") private class MaxPartitionToAdjacencyList extends BaseOperationMaxPartitionToAdjacencyListContext> implements AggregatorMaxPartitionToAdjacencyListContext> { public final String PARTITIONS_UPDATES_COUNTER_NAME = "Partitions updates"; public final String COUNTER_GROUP = "graphs"; public MaxPartitionToAdjacencyList() { super(new Fields("partition", "source", "list", "flags")); } @Override public void start( FlowProcess flowProcess, AggregatorCallMaxPartitionToAdjacencyListContext> aggregatorCall) { MaxPartitionToAdjacencyListContext context = new MaxPartitionToAdjacencyListContext(); context.source = aggregatorCall.getGroup().getInteger("source"); aggregatorCall.setContext(context); } @Override public void aggregate( FlowProcess flowProcess, AggregatorCallMaxPartitionToAdjacencyListContext> aggregatorCall) { MaxPartitionToAdjacencyListContext context = aggregatorCall.getContext(); TupleEntry arguments = aggregatorCall.getArguments(); int node = arguments.getInteger("node"); int partition = arguments.getInteger("partition"); boolean flag = arguments.getBoolean("flag"); if (context.partition == -1) { context.partition = partition; } else { if (flag && context.partition > partition) { flowProcess.increment(COUNTER_GROUP, PARTITIONS_UPDATES_COUNTER_NAME, 1); } } if (node != context.source) { context.targets.add(node); //here, convert boolean flags back to 1's or 0's context.flags.add((byte) (flag ? 1 : 0)); } } @Override public void complete( FlowProcess flowProcess, AggregatorCallMaxPartitionToAdjacencyListContext> aggregatorCall) { MaxPartitionToAdjacencyListContext context = aggregatorCall.getContext(); Tuple result = new Tuple( context.partition, context.source, StringUtils.joinObjects(",", context.targets), StringUtils.joinObjects(",", context.flags)); //Here's the flags aggregatorCall.getOutputCollector().add(result); } } @SuppressWarnings({ "serial", "rawtypes", "unchecked" }) private class MaxPartitionToTuples extends BaseOperation implements Buffer { public MaxPartitionToTuples() { super(new Fields("partition", "node", "source", "flag")); } @Override public void operate( FlowProcess flowProcess, BufferCall bufferCall) { IteratorTupleEntry> itr = bufferCall.getArgumentsIterator(); int maxPartition; TupleEntry entry = itr.next(); maxPartition = entry.getInteger("partition"); emitTuple(bufferCall, maxPartition, entry); while (itr.hasNext()) { entry = itr.next(); emitTuple(bufferCall, maxPartition, entry); } } private void emitTuple( BufferCall bufferCall, int maxPartition, TupleEntry entry) { Tuple result = new Tuple( maxPartition, entry.getInteger("node"), entry.getInteger("source"), entry.getBoolean("flag")); bufferCall.getOutputCollector().add(result); } } @SuppressWarnings({ "serial", "rawtypes" }) private class FanOut extends BaseOperation implements Function { public FanOut() { super(new Fields("partition", "node", "source", "flag")); } @Override public void operate( FlowProcess flowProcess, FunctionCall functionCall) { TupleEntry args = functionCall.getArguments(); int partition = args.getInteger("partition"); int source = args.getInteger("source"); Tuple result = new Tuple(partition, source, source, true); functionCall.getOutputCollector().add(result); String[] nodeList = args.getString("list").split(","); String[] flagList = args.getString("flags").split(","); for (int c = 0; c nodeList.length; c++) { //During fanout, we convert the flags to booleans result = new Tuple( partition, Integer.parseInt(nodeList[c]), source, Integer.parseInt(flagList[c]) != 0); functionCall.getOutputCollector().add(result); } } } }
The important things here are:
- The fact that this code is almost exactly the same as the one from the previous post.
- Except that it carries the flags around throughout the job.
- And that it uses the flag field in the sorting order of edges to make sure that it never picks the partition of an edge that has a 0 set as its flag.
The result
When we run the final algorithm against the graph, it will produce the following: