Einer der wichtigsten Schritte bei der Erstellung von Modellen des maschinellen Lernens zur Vorhersage molekularer Eigenschaften ist die Aufteilung unserer Daten in Trainings-, Validierungs- und Testsätze. Eine gut durchdachte Aufteilungsstrategie stellt sicher, dass unser Modell gut auf ungesehene Daten verallgemeinert und zuverlässige Leistungskennzahlen liefert. Oft sind wir nicht nur an einer einzigen Eigenschaft interessiert, sondern an der Vorhersage mehrerer Eigenschaften gleichzeitig. Nicht alle Eigenschaften sind gleich, einige sind in unseren Datensätzen häufiger vorhanden als andere. Wenn wir nicht richtig damit umgehen, kann dieses Ungleichgewicht zu verzerrten Modellen führen.
In diesem Blog-Beitrag erklären wir, warum es in Datensätzen für molekulare Eigenschaften ein Ungleichgewicht gibt, und untersuchen Strategien zur Validierung von Datensplits. Zusammenfassend lässt sich sagen, dass es zwei Hauptfaktoren gibt, die bei der Aufteilung von Daten für molekulare Eigenschaften zu berücksichtigen sind: die Datenverteilung und die Datenverfügbarkeit. Wir zeigen, wie Sie mit Hilfe des Kolmogorov-Smirnov-Tests prüfen können, ob die Datenverteilung in den verschiedenen Datensätzen ähnlich ist. Wir zeigen auch, wie Sie mit dem Proportionen z-Test prüfen können, ob die Datenverfügbarkeit ähnlich ist. Dadurch wird sichergestellt, dass unser Test- (und Validierungs-) Satz repräsentativ für den Trainingssatz ist, was zu einer zuverlässigeren Modellbewertung führt.
Die Daten verstehen
Wir werden mit Daten aus der Open Polymer Challenge arbeiten. Sie bestehen aus verschiedenen molekularen Strukturen, die als SMILES-Strings dargestellt sind, zusammen mit mehreren Zieleigenschaften, die wir vorhersagen möchten. Dazu gehören: - Glasübergangstemperatur (Tg) - fraktioniertes freies Volumen (FFV) - Wärmeleitfähigkeit (Tc) - Polymerdichte (De) - Trägheitsradius (Rg)
kaggle competitions download -c neurips-open-polymer-prediction-2025
Wenn wir uns die Verteilung dieser Eigenschaften ansehen, stellen wir fest, dass einige Eigenschaften in dem Datensatz häufiger vertreten sind als andere.
from pathlib import Path
import pandas as pd
csv_path = Path("./neurips-open-polymer-prediction-2025/train.csv")
train_df = pd.read_csv(csv_path)
train_df.drop(columns=["id", "SMILES"]).describe()
Verstehen von Datenverfügbarkeitsmustern
Es gibt zwei Möglichkeiten, Daten über molekulare Eigenschaften zu sammeln: durch physikalische Simulationen (auch bekannt als Molecular Dynamics (MD) Simulationen) und experimentelle Messungen. Je nach Methode gibt es verschiedene Herausforderungen bei der Erfassung von Polymereigenschaftsdaten. Die Verfügbarkeit von Daten über Polymereigenschaften variiert erheblich zwischen physikalischen Simulationen und experimentellen Messungen, wobei jede Eigenschaft einzigartige Herausforderungen bei der Datengenerierung mit sich bringt. Da der Open Polymer Challenge-Datensatz simulierte oder rechnerische Daten enthält, konzentrieren wir uns hier auf das Verständnis der Auswirkungen der rechnerischen Herausforderungen und deren Einfluss auf die Verfügbarkeit von Daten für verschiedene Eigenschaften. Im Anhang geben wir einen Überblick über die Herausforderungen der experimentellen Datengenerierung.
Physikalische Simulation Datengenerierung
Für physikalische Simulationen ist die Datengenerierung wie folgt möglich: Trägheitsradius ≈ Dichte > fraktioniertes freies Volumen > Glasübergangstemperatur > Wärmeleitfähigkeit, je nach Rechenanforderungen und methodischer Komplexität.
Glasübergangstemperatur (Tg) - Mäßige Komplexität
Physikalische Simulationen können mit Hilfe von Molekulardynamik (MD)-Methoden zuverlässig Daten zur Glasübergangstemperatur erzeugen, allerdings mit einigen wichtigen Einschränkungen. Die Bestimmung der Glasübergangstemperatur in MD-Simulationen beinhaltet Abhängigkeiten von der Abkühlungsrate und systematische Temperaturabweichungen[1, 2].
Das Berechnungsprotokoll beinhaltet die Analyse von Dichte und Temperatur während der Abkühlungssimulationen, wobei Tg aus dem Schnittpunkt zweier linearer Anpassungen der Dichte-Temperatur-Kurve ermittelt wird[1, 3]. Trotz des systematischen Versatzes können MD-Simulationen erfolgreich relative Trends erfassen und konsistente Einstufungen von Polymer-Tg-Werten liefern[3, 4].
Fractional Free Volume (FFV) - Hohe rechnerische Durchführbarkeit
FFV ist eine der am leichtesten zugänglichen Eigenschaften für die rechnerische Generierung, da bereits umfangreiche Hochdurchsatz-Molekulardynamik-Datensätze verfügbar sind[5, 6, 7]. Die computergestützte FFV-Bestimmung verwendet geometrische Analysemethoden wie die Delaunay-Tesselierung oder das Einsetzen von Sondenpartikeln, um den Hohlraum in Polymerstrukturen zu quantifizieren[5, 7, 8].
Jüngste Studien haben FFV-Daten für Tausende von Polymeren durch automatisierte MD-Simulationsprotokolle erzeugt. Ma et al. erstellten Datensätze mit über 6.500 Homopolymeren und 1.400 Polyamiden[5], während Wang et al. Datensätze mit 1.683 Polymeren entwickelten, die dann zum Screening von über 1 Million hypothetischer Strukturen verwendet wurden[6]. Die Berechnungsmethode bietet eine hervorragende Skalierbarkeit für Hochdurchsatz-Screening-Anwendungen.
Wärmeleitfähigkeit (Tc) - rechenintensiv, aber machbar
Die Berechnung der Wärmeleitfähigkeit durch MD-Simulationen ist rechenintensiv, aber gut etabliert[9, 10, 11, 12]. Die Eigenschaft erfordert Gleichgewichts-Molekulardynamiksimulationen mit sorgfältiger Berücksichtigung der Effekte der Systemgröße und langen Simulationszeiten, um statistische Konvergenz zu erreichen[10, 12].
In Hochdurchsatzstudien wurden erfolgreich Wärmeleitfähigkeitsdaten für Hunderte von Polymeren erzeugt[10, 11, 12]. Ma et al. berechneten die Wärmeleitfähigkeit für 365 Polymere mithilfe von MD-Simulationen und nutzten diese Daten dann zum Trainieren von maschinellen Lernmodellen für das Screening größerer Datenbanken[10]. Der Rechenaufwand ist höher als bei FFV-Berechnungen, bleibt aber für den Aufbau umfangreicher Datensätze machbar.
Polymer-Dichte (De) - Einfache Berechnung
Die Dichte ist bei MD-Simulationen rechnerisch einfach zu ermitteln[13, 14]. Sie erfordert standardmäßige NPT-Ensemblesimulationen (konstanter Druck und Temperatur), bei denen die Dichte aus der Masse und dem Volumen der Simulationszelle berechnet wird[13]. Das automatisierte RadonPy-System hat erfolgreiche Hochdurchsatz-Dichteberechnungen für über 1.000 einzigartige Polymere gezeigt[13].
Dichteberechnungen zeigen eine gute Übereinstimmung mit experimentellen Werten, wenn geeignete Äquilibrierungsprotokolle befolgt werden[13]. Die größte Herausforderung besteht darin, eine ordnungsgemäße Äquilibrierung zu erreichen, insbesondere bei komplexen Polymersystemen, die längere Glühvorgänge erfordern können[14].
Trägheitsradius (Rg) - Leicht zu berechnen
Der Trägheitsradius ist eine der zugänglichsten Eigenschaften in MD-Simulationen[13, 15, 16]. Er wird direkt aus den Atomkoordinaten mit Hilfe einer einfachen mathematischen Formel berechnet, die die Verteilung der Masse um den Massenschwerpunkt misst[13, 16]. Die Berechnung erfordert einen minimalen Rechenaufwand und kann aus jeder äquilibrierten Polymerstruktur gewonnen werden.
Rg dient als wichtiges Gleichgewichtskriterium bei Polymersimulationen, mit typischen Konvergenzanforderungen von weniger als 1% relativer Standardabweichung[13]. Diese Eigenschaft wird in Polymersimulationsstudien routinemäßig berechnet und stellt keine nennenswerten rechnerischen Hindernisse dar.
Zu kontrollierende Faktoren
Zusätzlich zu der üblichen Praxis, die Verteilung der Zieleigenschaften zu kontrollieren, müssen wir also auch die Verfügbarkeit der verschiedenen Eigenschaften berücksichtigen.
Testen für die Verteilung
Wir testen, ob es einen Unterschied zwischen der Zug- und der Testverteilung gibt, indem wir den Kolmogorov-Smirnov-Test verwenden.
from scipy.stats import ks_2samp
def ks_test_feature(set_a, set_b):
stat, p_value = ks_2samp(set_a.dropna(), set_b.dropna())
return stat, p_value
Testen auf Datenverfügbarkeit
Um den Unterschied im Anteil der fehlenden Werte zwischen zwei Gruppen zu testen, können wir den Proportionen z-Test verwenden.
from statsmodels.stats.proportion import proportions_ztest
def run_proportions_ztest(set_a, set_b):
counts = np.array([set_a.notnull().sum(), set_b.notnull().sum()])
nobs = np.array([set_a.size, set_b.size])
stat, pval = proportions_ztest(counts, nobs)
return stat, pval
Aufteilung der Daten
Wir laden die Trainingsdaten der Open Polymer Challenge und teilen sie in einen Trainings- (80%), einen Validierungs- (10%) und einen Testsatz (10%) auf. Da für einige Eigenschaften nur begrenzte Daten zur Verfügung stehen und wir genügend Trainingsbeispiele benötigen, um daraus zu lernen und die Notwendigkeit eines erneuten Trainings auf dem gesamten Datensatz zu begrenzen, verwenden wir eine 80-10-10-Aufteilung. Wenn Sie weniger datenhungrige Methoden verwenden, kann auch 60-20-20 eine Option sein. Da wir auf die Ähnlichkeit der Datenverteilung und -verfügbarkeit testen, stellen wir sicher, dass die Aufteilung repräsentativ ist und wir mit weniger Beispielen in den Validierungs- und Testsätzen auskommen können.
import pandas as pd
from sklearn.model_selection import train_test_split
# 1. split off 10% for dev_test
temp_df, dev_test = train_test_split(
train_df,
test_size=0.1,
random_state=SEED,
shuffle=True
)
# 2. split the remaining 90% into 80% train and 10% valid
dev_train, dev_val = train_test_split(
temp_df,
test_size=0.111, # 0.111 * 0.9 = 0.1 of the original
random_state=SEED,
shuffle=True
)
Beachten Sie, dass wir hier Zufallsstichproben verwenden, da wir sicherstellen möchten, dass die Testmengen repräsentativ für die gesamte Datenverteilung sind. Eine alternative Strategie für die Aufteilung von Moleküldaten ist die Gerüstaufteilung, die sicherstellt, dass die chemischen Gerüste in der Testmenge nicht in der Trainingsmenge vorhanden sind. Die Idee dahinter ist, die Fähigkeit des Modells zur Generalisierung auf völlig neue chemische Strukturen zu testen. Es gibt zwar Python-Pakete, die es einfach aussehen lassen, aber
Testen Sie, ob die Verteilung ähnlich ist
Wir versuchen es zunächst mit SEED=42 und prüfen, ob die Verteilung der verschiedenen Eigenschaften zwischen dem Trainings- und dem Testsatz ähnlich ist:
for feature in dev_train.drop(columns=["id", "SMILES"]).columns:
stat, p_value = ks_test_feature(dev_train[feature], dev_test[feature])
print(f"K-S Test for {feature}: Statistic={stat:.4f}, p-value={p_value:.4f}")
SEED=42
K-S Test for Tg: Statistic=0.1779, p-value=0.1948
K-S Test for FFV: Statistic=0.0212, p-value=0.9299
K-S Test for Tc: Statistic=0.0893, p-value=0.7483
K-S Test for Density: Statistic=0.0833, p-value=0.8756
K-S Test for Rg: Statistic=0.1543, p-value=0.1895
Alle p-Werte liegen über 0,05, was bedeutet, dass wir die Nullhypothese, dass die beiden Stichproben aus der gleichen Verteilung stammen, nicht zurückweisen können. Mit anderen Worten, die Verteilungen der Eigenschaften in den Sets dev_train und dev_test sind ähnlich genug.
Das können wir durch eine visuelle Inspektion der Verteilungen bestätigen: 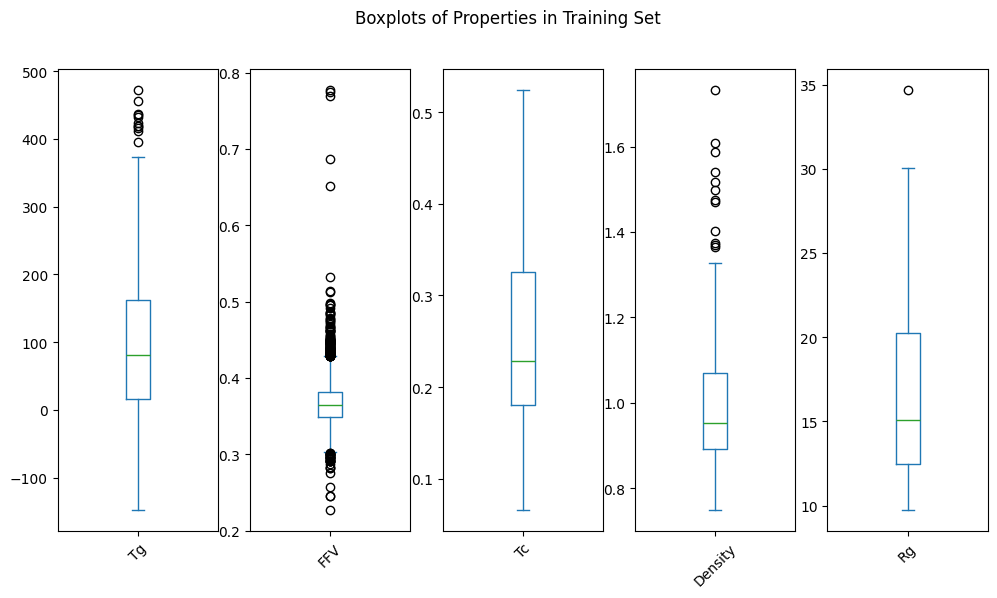
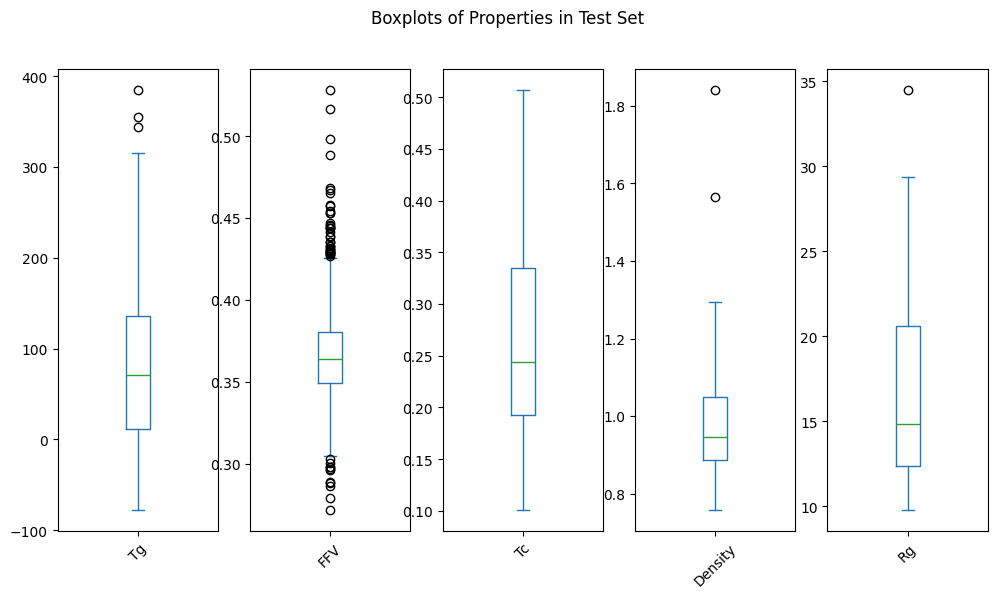
Testen Sie, ob die Datenverfügbarkeit ähnlich ist
Als Nächstes prüfen wir, ob die Datenverfügbarkeit zwischen dem Trainings- und dem Testsatz ähnlich ist:
for feature in dev_train.drop(columns=["id", "SMILES"]).columns:
stat, pval = run_proportions_ztest(dev_train[feature], dev_test[feature])
print(f"Proportions Z-Test for {feature}: Statistic={stat:.4f}, p-value={pval:.4f}")
SEED=42
Proportions Z-Test for Tg: Statistic=1.9714, p-value=0.0487
Proportions Z-Test for FFV: Statistic=-2.2804, p-value=0.0226
Proportions Z-Test for Tc: Statistic=1.9360, p-value=0.0529
Proportions Z-Test for Density: Statistic=1.4778, p-value=0.1395
Proportions Z-Test for Rg: Statistic=1.3515, p-value=0.1765
Hier sehen wir, dass die p-Werte für Tg und FFV unter 0,05 liegen, was bedeutet, dass wir die Nullhypothese ablehnen, dass die Anteile der fehlenden Werte in beiden Sets gleich sind. Mit anderen Worten, die Verfügbarkeit von Tg- und FFV-Daten unterscheidet sich signifikant zwischen den Trainings- und den Testsätzen.
Das können wir bestätigen, wenn wir uns die Anteile der fehlenden Werte ansehen:
Wir versuchen es erneut mit SEED=0:
SEED=0
Proportions Z-Test for Tg: Statistic=0.1784, p-value=0.8584
Proportions Z-Test for FFV: Statistic=-1.3942, p-value=0.1633
Proportions Z-Test for Tc: Statistic=0.0657, p-value=0.9476
Proportions Z-Test for Density: Statistic=-1.3214, p-value=0.1864
Proportions Z-Test for Rg: Statistic=-1.3214, p-value=0.1864
Diesmal liegen alle p-Werte über 0,05, was darauf hindeutet, dass die Anteile der fehlenden Werte in beiden Sets ähnlich sind.
Fazit
Bei der Aufteilung von Daten für molekulare Eigenschaften, insbesondere wenn es sich um mehrere Eigenschaften mit unterschiedlichen Repräsentationsniveaus handelt, ist es entscheidend sicherzustellen, dass sowohl die Verteilung der Eigenschaften als auch die Muster der fehlenden Werte in den Trainings-, Validierungs- und Testmengen ähnlich sind. Wir haben gezeigt, wie man den Kolmogorov-Smirnov-Test zum Vergleich von Verteilungen und den Proportionen z-Test zum Vergleich der Verfügbarkeit verwendet.
Wir haben die beobachteten Muster in den Datensätzen für Polymereigenschaften erklärt, bei denen bestimmte Eigenschaften wesentlich mehr fehlende Werte aufweisen als andere. Die rechnerischen Vorteile für FFV und Rg in Verbindung mit den experimentellen Einschränkungen für diese Eigenschaften führen zu Datensätzen, die stark auf simulierte Daten für diese Eigenschaften ausgerichtet sind.
Der nächste Schritt besteht darin, Ihr Modell zu trainieren und seine Leistung in den Validierungs- und Testgruppen zu bewerten. Das Thema Training von ML-Modellen für die Vorhersage von Moleküleigenschaften geht zwar über den Rahmen dieses Blogbeitrags hinaus, aber wir möchten Sie ermutigen, über die Metrik nachzudenken, mit der Sie diese Modelle bewerten. Angesichts der Erkenntnisse aus diesem Beitrag könnte eine gewichtete Metrik, die die unterschiedliche Verfügbarkeit von Eigenschaften berücksichtigt, besser geeignet sein als ein einfacher Durchschnitt.
Anhang
Welche Sets sollen verglichen werden?
Beachten Sie, dass der Unterschied zwischen der Trainings- und der Testverteilung verglichen wird und nicht eine der Teilmengen mit dem gesamten Datensatz verglichen wird. Die Teststatistik geht von unabhängigen Stichproben aus. Wäre die eine Menge eine Teilmenge der anderen, wäre diese Annahme verletzt.
Vollständigkeit
Der Vollständigkeit halber haben wir auch die Kolmogorov-Smirnov-Teststatistik und den p-Wert bei SEED=0 berechnet:
SEED=0
K-S Test for Tg: Statistic=0.0808, p-value=0.9137
K-S Test for FFV: Statistic=0.0220, p-value=0.9102
K-S Test for Tc: Statistic=0.1284, p-value=0.2133
K-S Test for Density: Statistic=0.1112, p-value=0.3953
K-S Test for Rg: Statistic=0.1612, p-value=0.0708
Auch hier liegen alle p-Werte über 0,05, was bedeutet, dass wir die Nullhypothese, dass die beiden Stichproben aus der gleichen Verteilung stammen, nicht zurückweisen können.
Herausforderungen bei der experimentellen Datengenerierung
Es lohnt sich, auch die experimentellen Herausforderungen zu verstehen, da sie sich von den rechnerischen unterscheiden und es auch experimentelle Datensätze gibt. Experimentelle Methoden stehen vor zunehmenden Herausforderungen in der Reihenfolge: Dichte < Wärmeleitfähigkeit < Glasübergangstemperatur < fraktioniertes freies Volumen < Trägheitsradius. Daher können Eigenschaften wie Dichte und Wärmeleitfähigkeit trotz der rechnerischen Zugänglichkeit eine bessere experimentelle Darstellung aufweisen.
Glasübergangstemperatur (Tg) - Bedeutende experimentelle Herausforderungen
Die experimentelle Tg-Bestimmung stößt auf erhebliche Schwierigkeiten, insbesondere bei starren konjugierten Polymeren[17, 18, 19]. Herkömmliche Methoden der Differential-Scanning-Kalorimetrie (DSC) versagen oft bei der Erkennung eindeutiger Glasübergänge in konjugierten Donor-Akzeptor-Polymeren aufgrund der extrem kleinen Änderungen der spezifischen Wärmekapazität (Δcp)[17, 19]. Die Werte können von 0,28 J-g-¹K-¹ für flexible Polymere wie Polystyrol auf 10-³ J-g-¹K-¹ für starre konjugierte Polymere fallen[17].
Die Herausforderungen ergeben sich aus der starren Struktur des Rückgrats und der teilkristallinen Natur vieler Polymere, die das Ausmaß der thermischen Signaturen verringern[17, 19]. Experimentelle Protokolle erfordern spezielle Techniken wie physikalische Alterungsexperimente, Studien zur Abhängigkeit von der Abkühlungsrate und ergänzende dynamische mechanische Analysen zur Bestätigung der Tg-Werte[18, 19].
Computergestützt vs. Experimentell
Simulierte Tg-Werte überschätzen die experimentellen Messungen in der Regel um 80-120 K, da die Abkühlungsraten in Simulationen (10⁹ K/s) viel schneller sind als in Experimenten (10-²-10-¹ K/s)[1]. Berücksichtigen Sie dies, wenn Sie simulierte und experimentelle Tg-Daten kombinieren.
Fractional Free Volume (FFV) - Indirekte experimentelle Methoden
Die experimentelle FFV-Bestimmung beruht auf indirekten Methoden mit erheblichen Einschränkungen[7, 8]. Die Positronen-Annihilations-Lebensdauer-Spektroskopie (PALS) liefert relative Messungen, erfordert jedoch eine Kalibrierung und beinhaltet Annahmen über die Hohlraumform
Jüngste Fortschritte haben Bondis Gruppenbeitragsmethode aktualisiert, aber die experimentelle Validierung bleibt eine Herausforderung, da direkte Messverfahren für das freie Volumen erforderlich sind[7]. Die semi-empirische Natur der experimentellen Ansätze führt zu Unsicherheiten bei den absoluten FFV-Werten.
Wärmeleitfähigkeit (Tc) - Messkomplexität
Die Messung der Wärmeleitfähigkeit von Polymeren stellt eine große experimentelle Herausforderung dar[20, 21, 22]. Diese Eigenschaft ist für polymere Flüssigkeiten und Feststoffe "notorisch schwer zu messen"[22]. Zu den wichtigsten Herausforderungen gehören die Eliminierung von Konvektionseffekten, die Sicherstellung eines ordnungsgemäßen thermischen Kontakts und das Management von Temperaturgradienten[20, 21].
Die Messunsicherheiten können bei teilkristallinen Polymeren unter Atmosphärendruckbedingungen ±20,7% erreichen[20]. Die Komplexität steigt mit den für industrielle Anwendungen relevanten Verarbeitungsbedingungen, die spezielle Hochdruck- und Hochtemperaturgeräte erfordern[20]. Die Auswirkungen der Probenvorbereitung und der thermischen Vorgeschichte sorgen für zusätzliche Variabilität[21].
Polymerdichte (De) - Präzision und Probenherausforderungen
Die experimentelle Dichtemessung ist eine Herausforderung für die Präzision, insbesondere bei kleinen oder heterogenen Proben[23, 24]. Die Archimedes-Methode hat ihre Grenzen bei dünnwandigen Proben. Präzise Dichtemessungen erfordern eine sorgfältige Kontrolle von Temperatur, Feuchtigkeit und Probenvorbereitung[23, 24].
Variationen innerhalb der Proben und die Notwendigkeit einer repräsentativen Probenahme schaffen zusätzliche Komplikationen[23]. Für Polymersysteme unter Verarbeitungsbedingungen sind spezielle Druck-Volumen-Temperatur-Geräte (pvT) erforderlich, was die Komplexität und die Kosten erhöht[20].
Radius der Trägheit (Rg) - Begrenzter direkter experimenteller Zugang
Für den Trägheitsradius gibt es keine direkten experimentellen Messmethoden für Polymersysteme in Masse. Die Lichtstreuung kann zwar Rg-Informationen für Polymere in Lösung liefern, aber dies ist ein anderer Zustand als die für die meisten Anwendungen relevanten Eigenschaften von Massenpolymeren[16]. Kleinwinkel-Neutronenstreuung und Röntgenstreuung können strukturelle Informationen liefern, erfordern jedoch spezielle Einrichtungen und eine komplexe Dateninterpretation.
Die Eigenschaft ist in erster Linie durch Berechnungsmethoden zugänglich, wodurch eine erhebliche Datenlücke für die experimentelle Validierung von Simulationsvorhersagen entsteht.
Referenzen
Banner Bildnachweis: Lone Thomasky & Bits&Bäume / Distorted Lava Flow / Lizenziert durch CC-BY 4.0
Den Code finden Sie auf unserem GitHub.
Verfasst von

Jetze Schuurmans
Machine Learning Engineer
Jetze is a well-rounded Machine Learning Engineer, who is as comfortable solving Data Science use cases as he is productionizing them in the cloud. His expertise includes: AI4Science, MLOps, and GenAI. As a researcher, he has published papers on: Computer Vision and Natural Language Processing and Machine Learning in general.
Contact