Ein Modell zur Vorhersage, wann Covid-19 nachlässt

Wir wissen jetzt, dass wir mit Covid-19 leben müssen. Genauso wie wir gelernt haben, mit dem Grippevirus jedes Jahr zu leben. Aber die größere Frage, die sich alle stellen - Regierungen, Unternehmen, Organisationen, Gemeinden und Einzelpersonen weltweit - ist, wann das Virus auf ein erträgliches Maß zurückgehen wird.

Gibt es ein Vorhersagemodell für Covid 19, das vorhersagen kann, in wie vielen Tagen (Monaten) es enden wird? Es scheint, dass es ein Modell gibt, das dies kann. Dieses Modell wurde vom Nobelpreisträger Prof. Michael Levitt vorgeschlagen, der es mit großer Genauigkeit auf Daten aus Hubei und später auf Daten aus anderen Ländern anwandte. Das Levitt-Modell ist robust, einfach und zuverlässig, unabhängig von der Größe der Bevölkerung, den Testmöglichkeiten, den fehlenden Daten, der Untererfassung, der geografischen Region und der Frage, was ein Covid-19-Todesfall ist.

Wir haben es gerade auf die Covid-19-Daten des Bundesstaates Telangana (Indien) angewendet (Quelle: Wiki COVID-19_pandemic_in_Telangana), um zu sehen, wann sie in meinem Bundesstaat enden wird. Wir haben dies auf die Covid-Daten von Telangana vom 14. März 2020 bis zum 5. Juli 2020 angewendet . Dann haben wir eine Best Line Regression auf die Daten angewendet. Dann haben wir diese Best-Fit-Kurve extrapoliert, um zu sehen, wann der Virus abklingt.

In der Literatur wurde eine lineare Regression verwendet, um die beste Anpassung zu erzielen. Wir haben dies verbessert, um auch eine Potenzgesetzregression zu verwenden, die ein besserer Schätzer ist, da das Potenzgesetz in der Natur die Norm ist, im Gegensatz zu linearen Modellen.

Wir geben auch die R2-Werte der Regression an.

Lassen Sie uns zunächst das Levitt-Modell definieren, wie es vorgeschlagen wurde.

Levitt-Modell

Für die Erstellung des Modells haben wir die kumulativen Covid-19-Fälle und Todesfälle, wie sie uns gemeldet wurden.

Levitt-Modell nach Fällen (Trend : Lineare Regression)

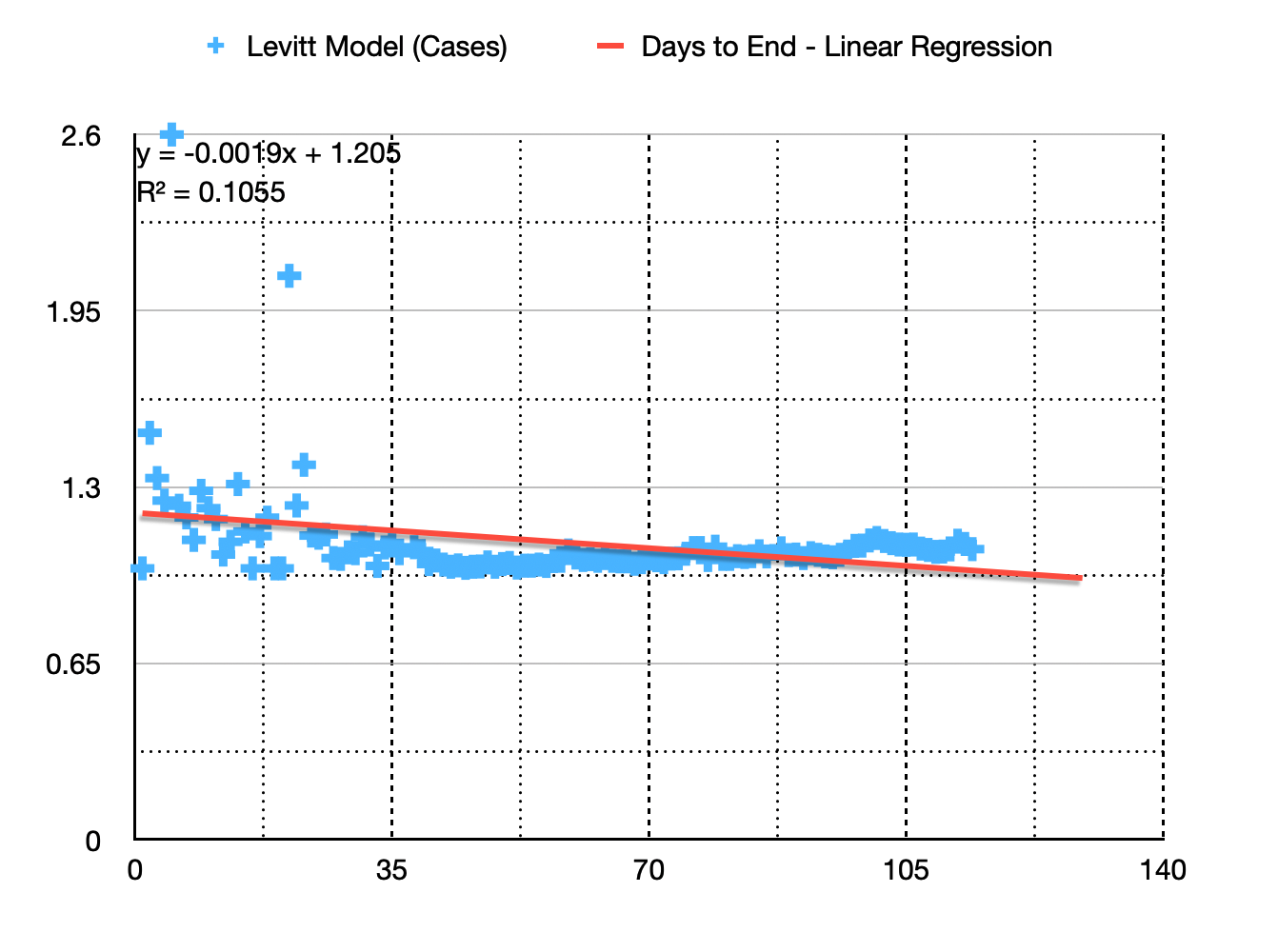
Wie Sie sehen, ist die Kurve der besten Anpassung durch lineare Regression eine gerade Linie, die durch die Gleichung :

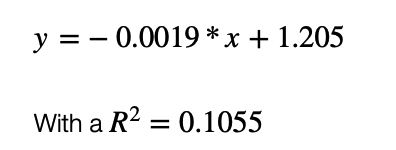
Dies ergibt die Tage bis zum Ende der Pandemie (ab dem ersten Todesfall): 107,40 ~ 108 Tage, was ungefähr dem 14. Juli 2020 entspricht (ungefähr jetzt)

Levitt-Modell nach Fällen (Trend : Power Law Regression)

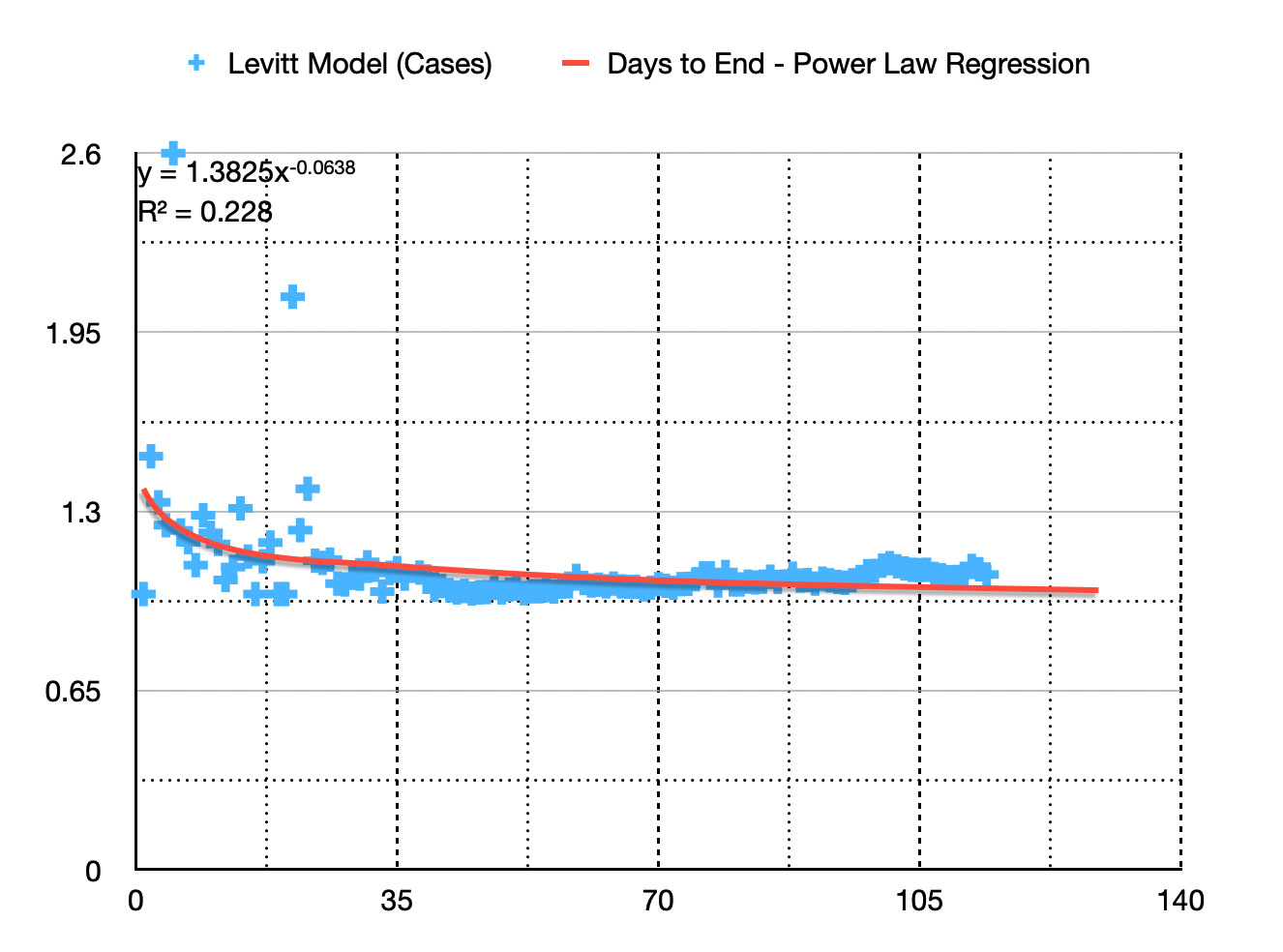Wie Sie sehen können, ist die Kurve der besten Anpassung durch Potenzgesetzregression eine Potenzgesetzfunktion, die durch die Gleichung definiert ist:

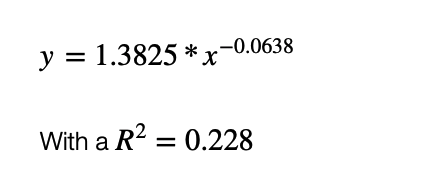
Daraus ergeben sich die Tage bis zum Ende der Pandemie (ab dem ersten Todesfall): 157,8 ~ 158 Tage, was etwa der 1. Septemberwoche (3. oder 4. September) entspricht, also etwa 44 Tage vom 20. Juli 2020!!!!!

Levitt-Modell nach Todesfällen (Trend : Lineare Regression)

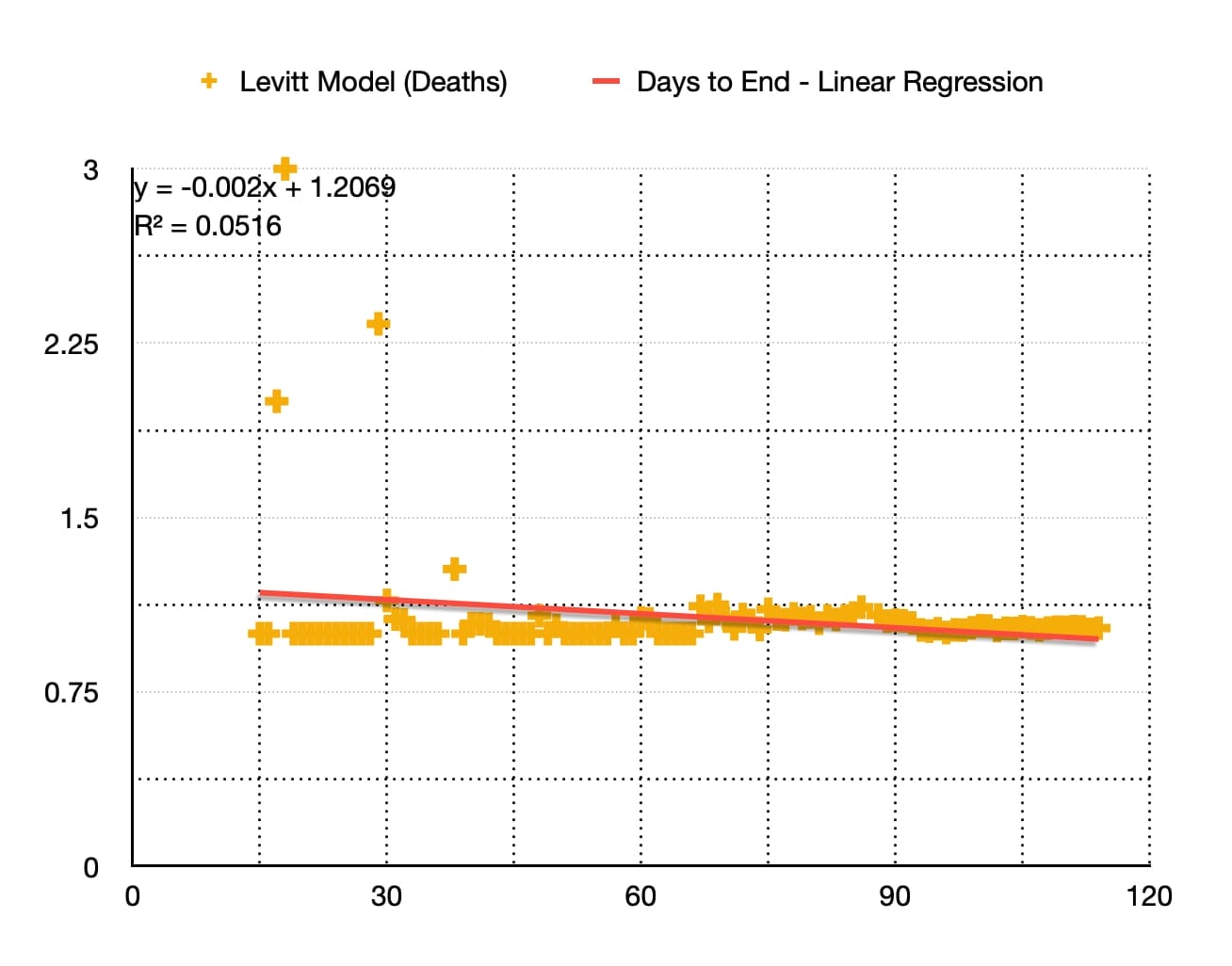Wie Sie sehen, ist die Kurve der besten Anpassung durch lineare Regression eine gerade Linie, die durch die Gleichung :

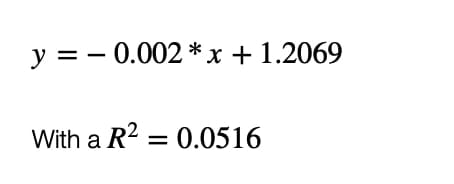
Daraus ergeben sich die Tage bis zum Ende der Pandemie (ab dem ersten Todesfall): 102,95 ~ 103 Tage, was ungefähr dem 9. Juli 2020 entspricht

Levitt-Modell nach Todesfällen (Trend :Power Law Regression)

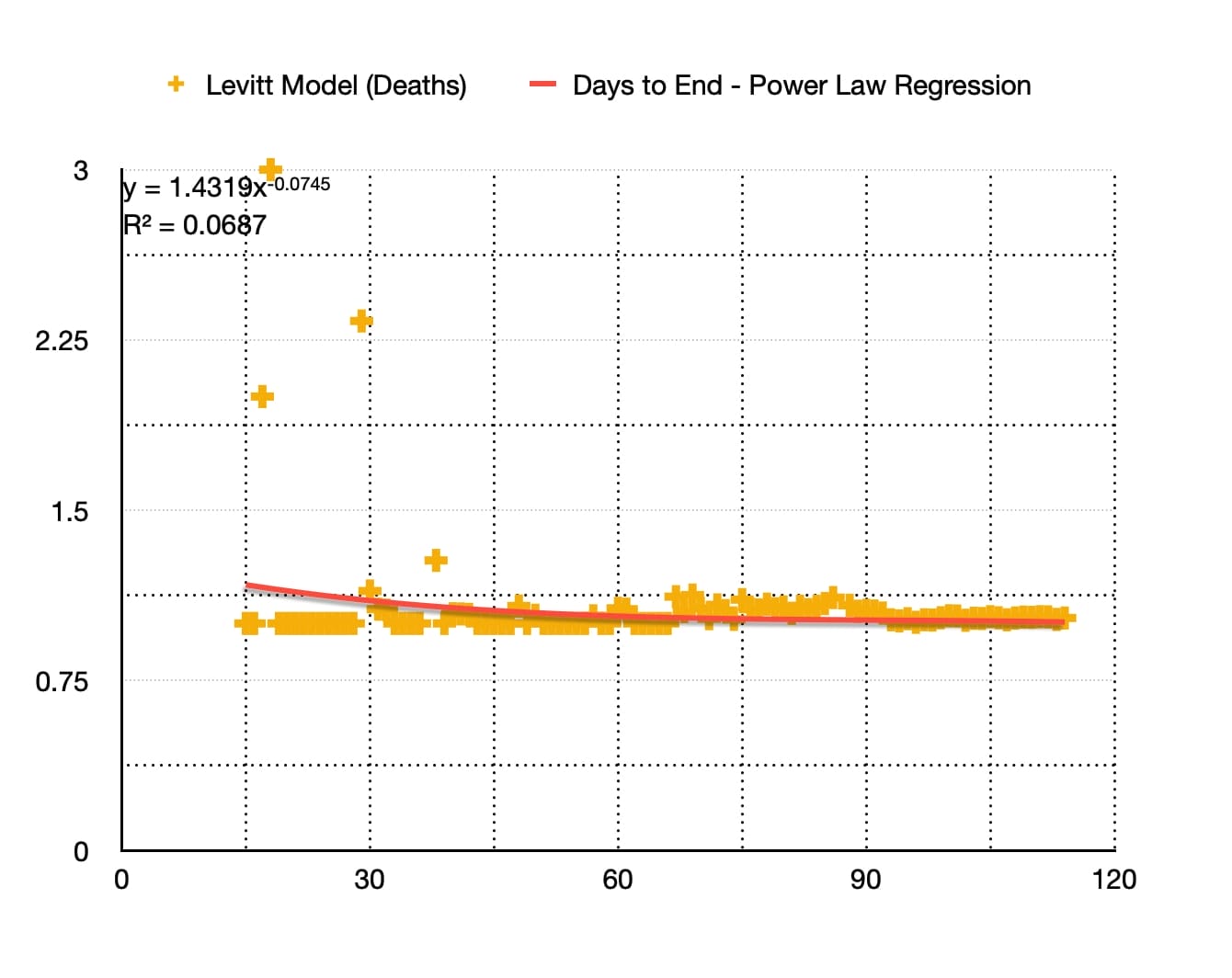Wie Sie sehen können, ist die Kurve der besten Anpassung durch Potenzgesetzregression eine Potenzgesetzfunktion, die durch die Gleichung definiert ist:

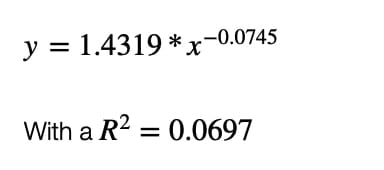
Dies ergibt die Tage bis zum Ende der Pandemie (ab dem ersten Todesfall): 122 Tage, d.h. um den 28. Juli 2020

Analyse

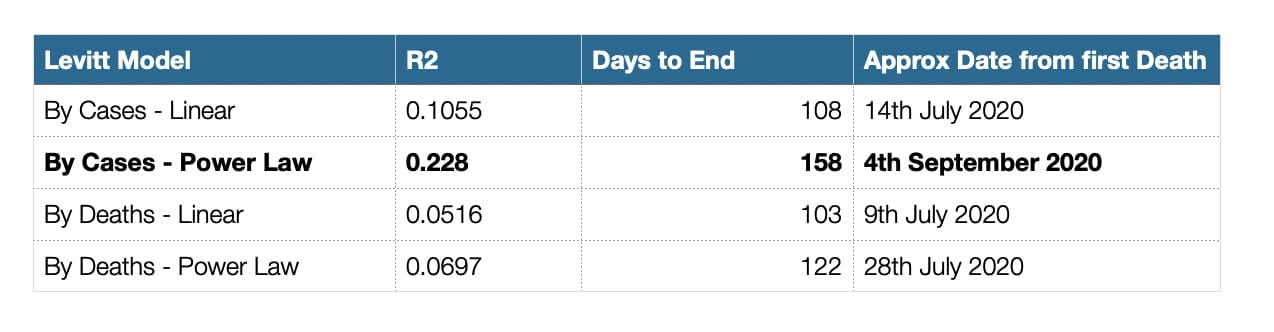Aus diesen Modellmetriken können wir Folgendes ableiten:

• In Telangana wird es höchstwahrscheinlich um die1. Septemberwoche 2020 herum abflauen. Etwa eineinhalb bis zwei Monate von jetzt an!!!!
• Die lineare Best-Fit-Trendlinie unterscheidet sich nicht wesentlich, wenn wir entweder Fälle oder Todesfälle für die Berechnung des Levitt-Modells verwenden. Die Koeffizienten der linearen Gleichung variieren nicht stark.
• Eine Potenzgesetz-Anpassung scheint genauer zu sein als eine lineare Anpassung. Das zeigt sich am R2-Wert (der die beste Anpassung misst). Dies stimmt auch mit unserer Hypothese überein, dass die Natur eher Potenzgesetzmodellen als linearen Modellen folgt. Daher sollten diese eher für die Extrapolation verwendet werden als lineare Modelle.
• Das Levitt-Modell nach Todesfällen scheint nicht genau zu sein. Möglicherweise sind die Todesfälle für die Schätzung des Modells nicht hoch korreliert.

Vorbehalte

• Wir haben nur Daten bis zum 5. Juli 2020.
• Alle Modelle sind nur so gut wie die Daten, die wir eingeben. Genauere und verifizierte Daten führen also zu genaueren Ergebnissen.
• Die Daten werden für bare Münze genommen, so wie sie gemeldet werden. Es wurde keine Überprüfung oder Validierung vorgenommen.

Über Uns

Sie können mich unter sai.panyam@idealantis.com oder sai.panyam@gmail.com für maßgeschneiderte Datenanalyse-, Modellierungs- und/oder KI/ML-Projekte erreichen. Wir sind immer auf der Suche nach interessanten Datensätzen, aus denen wir interessante und nützliche Erkenntnisse gewinnen können.

Anhang

Python-Code zur Ermittlung der Tage bis zum Ende der Pandemie

Nach Fällen

def TS_covid_levitt_linear_model(x): Rückgabe -0,0019 * x + 1,205 def TS_covid_end_day_linear(y): return (1.205 - y)/0.0019 # Extrapolieren für Ht = 1.001 ts_end_days_linear = TS_covid_end_day_linear(1.001) print (ts_end_days_linear) def TS_covid_levitt_power_model(x): return 1.3825 * np.power(x, -0.0638) def TS_covid_end_day_power(y): return np.power((1.3825/y), 1.0/0.0638) # Extrapolieren für Ht = 1.001 ts_end_days_power = TS_covid_end_day_power(1.001) print (ts_end_days_power)

Nach Todesfällen

def TS_covid_levitt_linear_model_by_deaths(x): return -0.002 * x + 1.2069 def TS_covid_end_day_linear_by_deaths(y): return (1.2069 - y)/0.002 # Extrapolieren für das Ende der Pandemie ts_end_days_linear_by_deaths = TS_covid_end_day_linear_by_deaths(1.001) print (ts_end_days_linear_by_deaths) def TS_covid_levitt_power_model_by_deaths(x): return 1.4319 * np.power(x, -0.0745) def TS_covid_end_day_power_by_deaths(y): return np.power((1.4319/y), 1.0/0.0745) # Extrapolieren für das Ende der Pandemie ts_end_days_power_by_deaths = TS_covid_end_day_power_by_deaths(1.001) print (ts_end_days_power_by_deaths)