Mit der zunehmenden Verbreitung von Deep Learning-Anwendungen ist es wichtig zu verstehen, wie diese Modelle funktionieren. Hier zeige ich anhand einfacher und reproduzierbarer Beispiele, wie und warum tiefe neuronale Netzwerke leicht getäuscht werden können. Außerdem diskutiere ich mögliche Lösungen.

Es wurden mehrere Studien darüber veröffentlicht, wie man ein tiefes neuronales Netzwerk (DNN) überlisten kann. Die bekannteste Studie, die 2015 veröffentlicht wurde, verwendet evolutionäre Algorithmen oder Gradientenaufstieg, um die gegnerischen Bilder zu erzeugen.¹ Eine sehr aktuelle Studie (Oktober 2017) zeigte, dass ein DNN durch die Veränderung eines einzigen Pixels getäuscht werden kann.² Dieses Thema scheint unterhaltsam zu sein, hat aber erhebliche Auswirkungen auf aktuelle und zukünftige Anwendungen von Deep Learning. Ich glaube, dass es extrem wichtig ist zu verstehen, wie diese Modelle ticken, um robuste Deep Learning-Anwendungen zu entwickeln (und ein weiteres Ereignis wie die Random Forest-Manie zu vermeiden). ³

Eine umfassende und vollständige Zusammenfassung finden Sie im Blog When DNNs go wrong, den ich Ihnen empfehle zu lesen.

All diese erstaunlichen Studien verwenden modernste Deep Learning-Techniken, was es (meiner Meinung nach) schwierig macht, sie zu reproduzieren und Fragen zu beantworten, die wir als Nicht-Experten auf diesem Gebiet haben könnten.

Meine Absicht in diesem Blog ist es, die wichtigsten Konzepte auf den Boden der Tatsachen zu bringen, in ein leicht reproduzierbares Umfeld, in dem sie klar und tatsächlich sichtbar sind. Außerdem hoffe ich, dass dieser kurze Blog zu einem besseren Verständnis der Grenzen von diskriminierenden Modellen im Allgemeinen beitragen kann. Den vollständigen Code, der in diesem Blogbeitrag verwendet wurde, finden Sie hier.

Was ist diskriminierend?

Neuronale Netze gehören zur Familie der diskriminativen Modelle. Sie modellieren die Abhängigkeit einer unbeobachteten Variablen (Ziel) von einer beobachteten Eingabe (Merkmale). In der Sprache der Wahrscheinlichkeitsrechnung wird dieses Szenario durch die bedingte Wahrscheinlichkeit dargestellt und wie folgt ausgedrückt:

p(target|features)

lautet: die Wahrscheinlichkeit des Ziels angesichts der Merkmale (z.B. die Wahrscheinlichkeit, dass es aufgrund der gestrigen Wetter-, Temperatur- und Druckmessungen regnen wird).

Multinomiale logistische Regressionsmodelle gehören ebenfalls zu diesen diskriminativen Modellen und sind im Grunde ein neuronales Netzwerk ohne versteckte Schicht. Seien Sie bitte nicht enttäuscht, aber ich werde zunächst einige Konzepte anhand der multinomialen logistischen Regression demonstrieren. Dann werde ich die Konzepte auf ein tiefes neuronales Netzwerk ausweiten.

Täuschende multinomiale logistische Regression

Wie bereits erwähnt, kann eine multinomiale logistische Regression als ein neuronales Netzwerk ohne versteckte Schicht betrachtet werden. Es modelliert die Wahrscheinlichkeit, dass das Ziel (Y) einer bestimmten Kategorie (c) angehört, als eine Funktion (F), die von der linearen Kombination der Merkmale ()) abhängt. Wir schreiben dies als

P(Y=c|X)=F(theta_{c}^Tcdot X)

wobei $theta_c$ die Koeffizienten der linearen Kombination für jede Kategorie sind. Die durch das Modell vorhergesagte Klasse ist diejenige, die die höchste Wahrscheinlichkeit ergibt.

Wenn das Ziel Y binär ist, wird F als eine sigmoide Funktion verwendet, wobei die logistische Funktion am häufigsten verwendet wird. Wenn Y mehrklassig ist, verwenden wir in der Regel F als Softmax-Funktion.

Abgesehen vom konzeptionellen Verständnis diskriminativer Modelle ist es die lineare Kombination der Merkmale ($theta_{c}^Tcdot X$), die Klassifizierungsmodelle angreifbar macht, wie ich zeigen werde. Um es mit den Worten von Jedi-Meister Goodfellow zu sagen: "Lineares Verhalten in hochdimensionalen Räumen reicht aus, um negative Beispiele zu erzeugen". ⁴

Iris-Datensatz

Als ich darüber nachdachte, wie ich diesen Blogbeitrag verfassen und die Konzepte tatsächlich visualisieren könnte, kam ich zu dem Schluss, dass ich zwei Dinge brauche:

• Ein 2-dimensionaler Merkmalsraum.
• Ein Modell mit hoher Genauigkeit in diesem Bereich.

Der 2-dimensionale Raum, weil ich Diagramme erstellen wollte, die die Konzepte direkt zeigen. Hohe Genauigkeit, denn es ist bedeutungslos, wenn ich ein schlechtes Modell überlisten kann.

Zu meinem Glück stellt sich heraus, dass eine gute Genauigkeit im Iris-Datensatz erzielt werden kann, wenn nur zwei Merkmale beibehalten werden: Blütenblattlänge und Blütenblattbreite.

Wenn Sie alles in Form bringen, sehen die Daten folgendermaßen aus

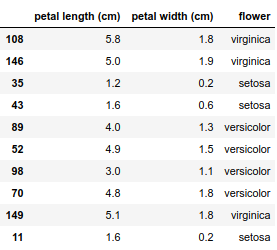
Dieser Datensatz enthält nur 150 Beobachtungen. Ich werde das Modell an alle Daten anpassen, indem ich eine Cross-Entropie-Verlustfunktion und einen L2-Regularisierungsterm verwende. Dies ist eine einfache Plug-and-Play-Anwendung aus dem fantastischen scikit-learn.

model = LogisticRegression(max_iter=100, solver='lbfgs', multi_class='multinomial', penalty='l2')
model.fit(X=iris.loc[:, iris.columns != 'flower'], y=iris.flower)

Die durchschnittliche Genauigkeit des Modells beträgt $96.6%$. Dieser Wert basiert auf den Trainingsdaten und kann irreführend sein. Selbst wenn ich einen Regularisierungsterm verwende, kann es zu einer Überanpassung kommen. ⁵

Schauen wir uns nun unsere Vorhersagen an und wie unser Modell die Klassifizierungsgrenzen zieht.

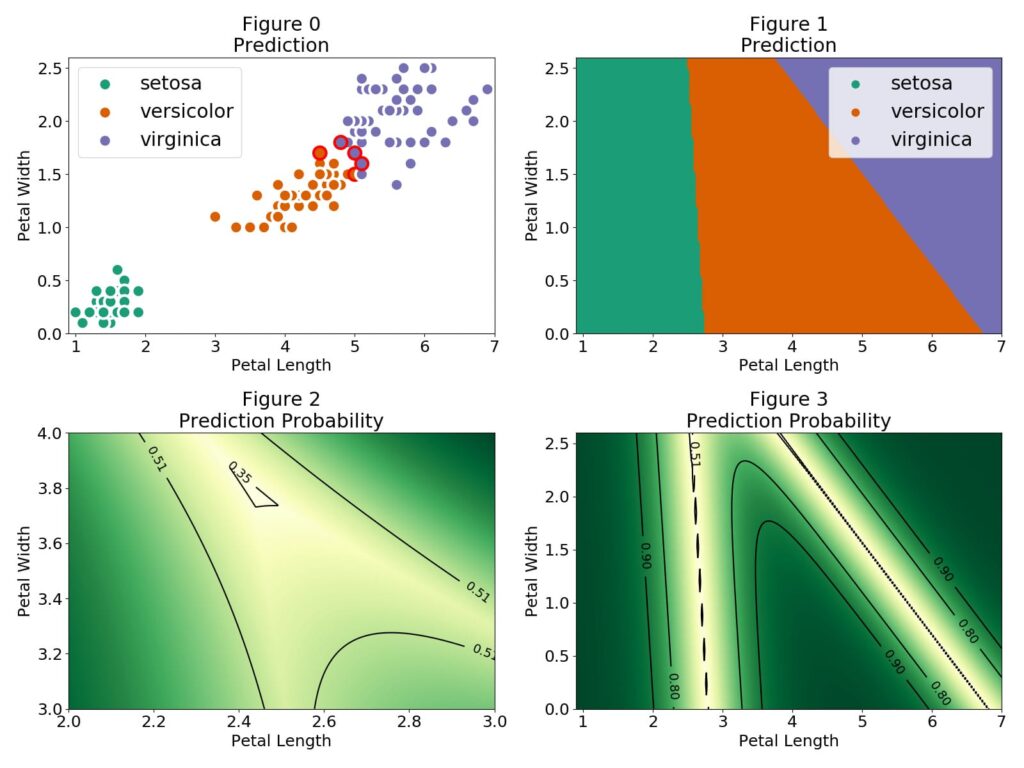
In Abbildung 0 kennzeichnen die roten äußeren Kreise die Beobachtungen, die falsch klassifiziert wurden. Die setosa-Blüten sind leicht zu identifizieren und es gibt eine Region, in der die versicolor- und virginica-Beobachtungen dicht beieinander liegen. In Abbildung 1 sehen wir die verschiedenen Regionen für jede Blumenkategorie. Die Regionen sind durch eine lineare Grenze getrennt. Dies ist eine Folge des verwendeten linearen Kombinationsmodells $P(Y=c|X)=F(theta_{c}^Tcdot X)F$ ist die logistische Funktion

F(theta_{c}^Tcdot X)=frac{1}{1 + e^{-theta_{c}^Tcdot X}}

und die Klassifizierungsgrenze ist durch P(Y=c|X)=frac{1}{2} theta_{c}^Tcdot X=0 gegeben. Bei eindimensionalen Merkmalen ist die Grenze ein einzelner Wert, bei zwei Merkmalen ist die Grenze eine einzelne Linie, bei drei Merkmalen eine Ebene und so weiter. In unserem Multinomialfall verwenden wir die Softmax-Funktion

F(theta_{c}^Tcdot X)=frac{e^{theta_{c}^Tcdot X}}{Sigma_{i=1}^Ne^{theta_{i}^Tcdot X}}

wobei die Summe über i im Nenner über alle möglichen Klassen des Ziels läuft. In den Regionen, in denen nur zwei Klassen eine nicht vernachlässigbare Wahrscheinlichkeit haben, vereinfacht sich die Softmax-Funktion auf die logistische Funktion. Daher ist die lineare Klassifizierungsgrenze zwischen zwei Regionen durch die Kontur P(Y=c|X)=frac{1}{2} P(Y=c|X)=frac{1}{3} gegeben, in der die Unsicherheit unserer Vorhersage maximal ist. Diese Region ist in Abbildung 2 dargestellt.

Dabei ist zu beachten, dass sich die Regionen auf Werte erstrecken, die sehr weit von den Beobachtungen entfernt sein können. Das heißt, wir können eine Blütenblattlänge von 1 und eine Blütenblattbreite von 4 nehmen und trotzdem als Setosa klassifiziert werden. Mehr noch, Abbildung 4 zeigt, dass wir sogar weit entfernt von unseren Beobachtungen Regionen mit extrem hoher Wahrscheinlichkeit finden können. Wir können sogar eine negative Blütenblattlänge verwenden!

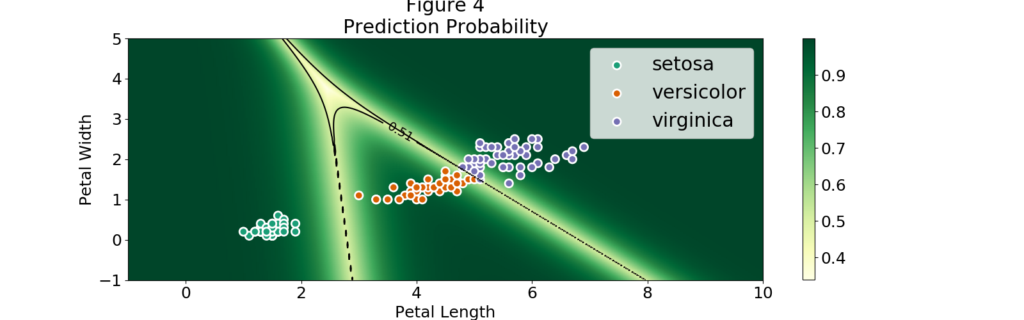
Lassen Sie uns einige Punkte aus Abbildung 4 auswählen und sehen, ob ich den multinomialen logistischen Klassifikator überlisten kann:

• Punkt: (.1, 5)
  • Vorhersage: setosa
  • Wahrscheinlichkeit: 0,998
• Punkt: (10, 10)
  • Vorhersage: virginica
  • Wahrscheinlichkeit: 1.0
• Punkt: (5, -5)
  • Vorhersage: versicolor
  • Wahrscheinlichkeit: 0,992

Machen Sie sich selbst ein Bild von Deep Learning!

Nehmen Sie an einem dreitägigen Kurs über Deep Learning teil. Der Kurs beginnt mit einer Einführung in die Hintergründe des Deep Learning und endet damit, dass Sie Ihre eigene Deep Learning-Anwendung erstellen. Er ist ideal für Datenwissenschaftler, die Erfahrung mit Python haben und mit unstrukturierten Daten wie Text, Bildern und Sprache arbeiten.