Zelluläre Automaten mit Rust: Teil I

In dieser dreiteiligen Serie und dem dazugehörigen Projekt werden wir elementare zelluläre Automaten mit Hilfe der Programmiersprache Rust und der Spiele-Engine Bevy zum Leben erwecken. Wir lernen ein paar Dinge über zelluläre Automaten, Rust, die Architektur von Entity-Component-Systemen und die grundlegende Spielentwicklung. Sie können die fertige Web-App online ausprobieren. Lassen Sie Ihrem Browser einen Moment Zeit, um die App herunterzuladen, und klicken Sie auf das Gitter, um der App den Fokus zu geben.

Ein zellularer Automat besteht aus einem regelmäßigen Gitter von Zellen, von denen jede genau einen aus einer endlichen Menge von Zuständen ausdrücken muss. Für jede Zelle bilden sie und ihre benachbarten Zellen ihre Nachbarschaft. Um hier Randbedingungen zu vermeiden, gehen wir davon aus, dass die beiden "Ränder" jeder Dimension benachbart sind. Ein zellulärer Automat kann eine beliebige Anzahl von Dimensionen haben, die nicht Null ist, und jede Dimension wird für die Identifizierung der Nachbarschaft einer Zelle berücksichtigt. Ein zellulärer Automat entwickelt sich im Laufe der Zeit nach einer Regel, die den nächsten Zustand jeder Zelle auf der Grundlage des aktuellen Zustands ihrer Nachbarschaft vorgibt. Der vollständige Satz der nächsten Zustände wird als nächste Generation bezeichnet. Die Evolutionsregel ist in der Regel einheitlich und im Laufe der Zeit unveränderlich, aber das ist nicht unbedingt erforderlich. In unserem Projekt kann der Benutzer die Simulation anhalten, um die Regeln zu ändern und sogar den Zustand der Zellen manuell umzuschalten.

Es macht uns Spaß, die Entwicklung von zellulären Automaten zu beobachten, aber zelluläre Automaten sind mehr als nur mathematisches Spielzeug. Sie zeigen, wie komplexes Verhalten auf natürliche Weise aus einem minimalen Zustand und einfachen Regeln entstehen kann. Insbesondere die Regel #110 ist Turing-komplett und in der Lage, ein universelles zyklisches Tag-System zu implementieren, das jede Turing-Maschine emulieren kann.

Diese Eleganz hat seit Jahrzehnten große Geister angezogen. Stanisław Ulam und John von Neumann entdeckten den zellulären Automaten in den 1940er Jahren während ihrer gemeinsamen Zeit am Los Alamos National Laboratory. 1970 stellte John Conway das Game of Life vor, den zweidimensionalen zellulären Automaten, der heute für seine Blöcke, Bienenstöcke, Boote, Blinklichter, Pulsare, Gleiter und Raumschiffe berühmt ist. 1982 veröffentlichte Conway einen Beweis für die Turing-Vollständigkeit und stellte den Automaten damit endlich auf die gleiche Stufe wie Turing-Maschinen und Lambda-Kalküle. Ebenfalls in den 1980er Jahren veröffentlichte Stephen Wolfram A New Kind of Science, in dem er systematisch elementare zelluläre Automaten untersuchte - eindimensionale zelluläre Automaten von nicht reduzierbarer Einfachheit. 1985 stellte Wolfram erstmals die Vermutung auf, dass die Regel Nr. 110 Turing-komplett ist, und 2004 veröffentlichte Matthew Cook den Beweis.

Elementare zelluläre Automaten

Einen elementaren zellulären Automaten stellt man sich normalerweise als eine einzelne Reihe von Zellen vor, von denen jede einen von zwei Zuständen ausdrücken muss: an, dargestellt durch eine schwarze Zelle, oder aus, dargestellt durch eine weiße Zelle. Wenn Sie bereits mit dem Spiel des Lebens vertraut sind, dann denken Sie vielleicht an on als lebendig und off als tot. Da das Spiel des Lebens jedoch zweidimensional ist, handelt es sich nicht um einen elementaren zellulären Automaten, also machen wir ohne ihn weiter.

Mehrere Generationen werden in der Regel als zweidimensionales Gitter dargestellt, so dass jede Zeile eine komplette Generation darstellt. Neue Generationen werden am Ende hinzugefügt, so dass die Entwicklung im Laufe der Zeit abwärts verläuft. Beachten Sie, dass dies willkürliche Entscheidungen sind, um die Visualisierung im Zeitverlauf zu unterstützen, und keine wesentlichen Eigenschaften des abstrakten Automaten. Um das Phänomen "Komplexität aus Einfachheit" besser untersuchen zu können, wird die Evolution häufig durch eine einzige feste Regel gesteuert. Diese Regel kodiert die vollständige Übergangstabelle für die acht möglichen Nachbarschaften.

Um zu verstehen, warum es acht mögliche Nachbarschaften gibt, lassen Sie uns die Nachbarschaft im eindimensionalen Raum betrachten. Wir definieren den Abstand zwischen zwei Zellen und auf natürliche Weise: als die Anzahl der Zellgrenzen, die auf dem Weg von nach überquert werden müssen. Außerdem definieren wir die Nachbarschaft einer Zelle als alle Zellen, deren Abstand von kleiner oder gleich eins ist. Für jede Zelle erhalten wir damit den linken Nachbarn, sich selbst und den rechten Nachbarn. Daraus folgt, dass jede Zelle dreimal betrachtet wird - einmal als Zentrum, einmal als linker Nachbar und einmal als rechter Nachbar.

Erinnern Sie sich nun daran, dass jede Zelle genau zwei Zustände ausdrücken kann, on und off. Unter Berücksichtigung der Zustände gibt es insgesamt 2³ = 8 mögliche Nachbarschaften. Wenn Sie X für on und • für off verwenden, lauten die acht möglichen Nachbarschaften und ihre Ordnungszahlen:

••• (0)
••X (1)
•X• (2)
•XX (3)
X•• (4)
X•X (5)
XX• (6)
XXX (7)

Eine Regel bestimmt das Ergebnis - on oder off - für jede Zelle als Folge ihres vorherigen Nachbarschaftsstatus. Da es acht mögliche Nachbarschaften gibt und jede Nachbarschaft einen von zwei resultierenden Zuständen erzeugen kann, gibt es 2⁸ = 256 mögliche Regeln. Der Ergebniszustand jeder Nachbarschaft kann auf ein einzelnes Bit in einer 8-Bit-Zahl abgebildet werden; diese Darstellungsstrategie wird gemeinhin als Wolfram-Kodierung bezeichnet. In einem Wolfram-Code entspricht jedes Bit, das mit bis nummeriert ist, einer der acht oben dargestellten möglichen Nachbarschaften. Das Vorhandensein eines 1 im ^dritten Bit bedeutet, dass die Nachbarschaft eine on Zelle erzeugt, während 0 bedeutet, dass die Nachbarschaft eine off Zelle erzeugt.

Betrachten wir Regel #206 als einen konkreten Fall. Zunächst konvertieren wir ins Binärformat, um zu erhalten:

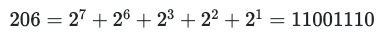
Wir können uns die Übergangstabelle so vorstellen:

                         Rule #206
bit index  =    7     6     5     4     3     2     1     0
binary     =    1     1     0     0     1     1     1     0
input      =   XXX   XX•   X•X   X••   •XX   •X•   ••X   •••
output     =    X     X     •     •     X     X     X     •

Nur zur Veranschaulichung beschränken wir den zellulären Automaten auf 30 Zellen. Wir können die Anfangsgeneration für unseren zellulären Automaten beliebig wählen, obwohl bestimmte Entscheidungen zu viel interessanteren Ergebnissen führen. Weil es interessant sein wird, beginnen wir mit nur einer Zelle, die den Zustand ausdrückt. Dann lassen wir Regel #206 für 9 Generationen laufen.

generation  1 = •••••••••••••••X••••••••••••••
generation  2 = ••••••••••••••XX••••••••••••••
generation  3 = •••••••••••••XXX••••••••••••••
generation  4 = ••••••••••••XXXX••••••••••••••
generation  5 = •••••••••••XXXXX••••••••••••••
generation  6 = ••••••••••XXXXXX••••••••••••••
generation  7 = •••••••••XXXXXXX••••••••••••••
generation  8 = ••••••••XXXXXXXX••••••••••••••
generation  9 = •••••••XXXXXXXXX••••••••••••••
generation 10 = ••••••XXXXXXXXXX••••••••••••••

Hier sind zwei coole Dinge passiert. Das eine ist leicht zu erkennen, buchstäblich: es wurde ein rechtwinkliges Dreieck gezeichnet. Das andere erfordert ein wenig Interpretation. Wir haben uns in diesem Beitrag schon oft auf binäre Kodierungen verlassen, also lassen Sie uns noch ein wenig nachsichtig sein. Wir können die Zellen von on als eine Kette von Binärziffern behandeln, so dass die Zelle ganz rechts on der^{Zahl 20} entspricht. Jetzt können wir die Generationen als Elemente einer Sequenz interpretieren:

1, 3, 7, 15, 31, 127, 511, 2047, 8191, 32767, …

Diese Reihe entspricht den Mersenne-Zahlen, wobei >= 1 ist:

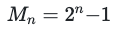
Andere Regeln erzeugen Entwicklungen mit verblüffenden Entsprechungen zu anderen mathematischen Entitäten, wie die Jacobsthal-Zahlen und das Pascalsche Dreieck. Und die Regeln #110 und #124 sind beide in der Lage, universelle Berechnungen durchzuführen.

Da wir nun wissen, was elementare zelluläre Automaten sind und warum sie interessant sein könnten, lassen Sie uns diese in Rust modellieren.

Modellierung elementarer zellulärer Automaten mit Rust

Es gibt ein Projekt, das auf diesem Blogbeitrag basiert. Es ist ziemlich einfach aufgebaut, ganz normal für eine einfache Binärkiste. Wenn ich einen Codeauszug präsentiere, entferne ich normalerweise alle Kommentare, aber Sie können alle Originalkommentare in dem Projekt auf GitHub sehen.

Das Datenmodell für den elementaren zellulären Automaten befindet sich in src/automata.rs zu finden, daher stammen alle Codeauszüge in diesem Abschnitt aus dieser Datei.

Schauen wir uns zunächst die Darstellung eines elementaren zellulären Automaten an.

Automaton, Konstante Generizität und bedingte Ableitung

Im Wesentlichen halten wir unsere Darstellungsstrategie supereinfach: Wir drücken einen elementaren zellulären Automaten als boolesches Array aus, wenn auch mit ein paar eleganten Spielereien, wie der bedingten Ableitung für Tests.

#[derive(Copy, Clone, Debug)]
#[cfg_attr(test, derive(PartialEq, Eq))]
pub struct Automaton<const K: usize = AUTOMATON_LENGTH>([bool; K]);

Unter Verwendung des newtype-Musters definieren wir eine 1-Element-Tupel-Struktur, um ein Array von K Booleans zu umhüllen. Anstatt die genaue Größe hart zu kodieren, bieten wir eine gewisse Flexibilität durch const generics. In Rust erstreckt sich die const-Generik über Werte von primitiven Typen und nicht über Typen oder Lebenszeiten. Wir setzen den const-Parameter auf AUTOMATON_LENGTH und machen den bloßen Typ Automaton äquivalent zu Automaton. An anderer Stelle setzen wir AUTOMATON_LENGTH selbst ein:

pub const AUTOMATON_LENGTH: usize = 64;

Da es sich bei AUTOMATON_LENGTH um Daten von const handelt, können wir sie verwenden, um den const-Parameter K zu erfüllen. Unsere Vorgabe Automaton wird also 64 Zellen umfassen, was für eine interessante Visualisierung ausreicht.

bool implementiert Copy, und Arrays implementieren Copy, wenn ihr Elementtyp dies tut. Wenn Sie diese Argumentationskette auf structs, tuples und struct tuples ausdehnen, kann unser newtype auch Copy implementieren, da sein einziges Feld Copy implementiert. Selbst wenn wir AUTOMATON_LENGTH in eine andere Zahl ändern würden, müsste diese klein genug sein, um eine sofortige Darstellung in der Anwendung zu unterstützen. Daher ist es effizient genug, Copy für Automaton abzuleiten.

Die Anwendung selbst ist nicht auf den Vergleich angewiesen, aber die Testsuite schon. Mit cfg_attr erhalten wir das Beste aus beiden Welten: Wir implementieren PartialEq und Eq nur beim Kompilieren und Linken der Test-Suite.

Beachten Sie, dass die natürliche Anordnung der Zellen innerhalb von Automaton dem Array selbst entspricht, d.h. die Zelle mit dem Index 0 ist die Zelle ganz links und die Zelle mit dem Index K - 1 ist die Zelle ganz rechts. Dies wird mehrmals von Bedeutung sein, da verschiedene Kontexte unterschiedliche natürliche Ordnungen implizieren und wir manchmal Koordinatentransformationen durchführen müssen, um dies zu berücksichtigen.

Nachfolge und const fn

Schauen wir uns nun die Methode next an, die die nächste Generation einer Automaton berechnet. Es gibt drei Fälle, mit denen next umgehen muss:

1. Die Berechnung der vorderen Randzelle, d.h. der Zelle ganz rechts, erfordert, dass die hintere Randzelle, d.h. die Zelle ganz links, als ihr rechter Nachbar behandelt wird. Mit anderen Worten, wir stellen uns den Automaten als eine Reihe vor, aber wir behandeln ihn wie einen Ring, der sich an den Enden herumdreht.
2. Die Berechnung der medialen Zellen, die trivial ist, sobald wir uns richtig orientiert haben.
3. Berechnung der Zelle für die hintere Kante, wobei die Zelle für die vordere Kante als ihr linker Nachbar behandelt werden muss.

impl<const K: usize> Automaton<K>
{
    pub fn next(&self, rule: AutomatonRule) -> Self
    {
        let mut next = [false; K];
        // Compute the leading edge cell, treating the final cell of the
        // automaton as its right neighbor.
        let ordinal = compute_ordinal(self[1], self[0], self[K - 1]);
        next[0] = rule.next_cell(ordinal);
        // Computing the medial cells is trivial.
        for i in 1 ..= K - 2
        {
            let ordinal = compute_ordinal(
                self[i + 1],
                self[i],
                self[i - 1]
            );
            next[i] = rule.next_cell(ordinal);
        }
        // Compute the trailing edge cell, treating the initial cell of the
        // automaton as its left neighbor.
        let ordinal = compute_ordinal(self[0], self[K - 1], self[K - 2]);
        next[K - 1] = rule.next_cell(ordinal);
        Automaton(next)
    }
}

compute_ordinal ist eine konstante Funktion, die die Ordnungszahl der Bevölkerung für die Nachbarschaft einer Zelle bestimmt. Um die Funktion unabhängig von der Identität einer bestimmten Zelle zu machen, akzeptiert sie den explodierten Nachbarschaftsstatus und antwortet auf die Ordnungszahl der Bevölkerung.

#[inline]
const fn compute_ordinal(left: bool, middle: bool, right: bool) -> u8
{
    let left = if left { 4u8 } else { 0 };
    let middle = if middle { 2u8 } else { 0 };
    let right = if right { 1u8 } else { 0 };
    let ordinal = left | middle | right;
    // Note that we cannot test range containment directly here because
    // `contains` is not a `const fn`.
    assert!(ordinal <= 7);
    ordinal
}

Übrigens kann eine const-Funktion zur Kompilierzeit verwendet werden, um const-Daten zu initialisieren. Const Rust ist eine faltbare Untermenge von Rust, die nur mit Literalen, const-Daten und von const-Funktionen erzeugten Werten arbeitet. Der Compiler wertet const-Ausdrücke aus und faltet sie zu einem einzigen Ergebnis zusammen. Durch die Verwendung von const-Funktionen kann sich Ihre Initialisierungslogik auf die Semantik und nicht auf magische Zahlen konzentrieren. Der Umfang von Const Rust ist immer noch begrenzt - es kann zum Beispiel noch keine Schleifen verarbeiten - aber es hat über viele Versionen hinweg immer mehr Funktionen erhalten. Eine gute Faustregel ist es, Daten und Funktionen wo immer möglich konstant zu machen, da dies Ihr Vokabular zur Kompilierzeit erweitert und somit die Ausdruckskraft Ihrer const und statischen Initialisierungen verbessert.

Richtig, zurück zu next. Bewaffnet mit der Ordnungszahl der Bevölkerung können wir die Methode (siehe unten) aufrufen, um die mitgelieferte Regel aufzufordern, den passenden Nachfolger für die entsprechende Nachbarschaft zu erzeugen. Danach müssen wir nur noch die Slots des gleichnamigen Arrays next auslesen und dann ein Automaton darum wickeln, bevor wir zurückkehren.

Regeln

AutomataRule stellt eine evolutionäre Regel dar, wiederum unter Verwendung des newtype-Musters. Dieser newtype umhüllt einen Wolfram-Code, ausgedrückt als u8.

#[derive(Copy, Clone, Default, Debug, PartialEq, Eq, PartialOrd, Ord, Resource)]
pub struct AutomatonRule(u8);

Resource Eigenschaft

Anmerkung: Wir leiten hier eine Reihe von Standard-Rust-Eigenschaften ab, aber Resource hebt sich von ab. Resource ist eine ableitbare Eigenschaft, die von Bevy, der einen Typ bezeichnet, der als globale Ressource verwendet werden kann. Mehr dazu im nächsten Blogbeitrag.

Nun schauen wir uns next_cell an, was völlig unkompliziert ist:

impl AutomatonRule
{
    #[inline]
    const fn next_cell(self, ordinal: u8) -> bool
    {
        self.0 & (1 << ordinal) != 0
    }
}

Erinnern Sie sich daran, dass der Wolfram-Code die komplette Übergangstabelle für einen elementaren zellulären Automaten mit nur acht Bits spezifiziert, so dass es eine einfache Angelegenheit ist, das Bit zu extrahieren, das mit einer Ordnungszahl der Bevölkerung verbunden ist. Es handelt sich lediglich um eine Bitverschiebung, ein bitweises Und und einen Test gegen Null.

Instanziieren einer Automaton

Wir brauchen einen sauberen Weg, um eine Automaton zu befüllen:

impl<const K: usize> From<u64> for Automaton<K>
{
    fn from(value: u64) -> Self
    {
        assert!(K <= 0u64.count_zeros() as usize);
        let mut next = [false; K];
        for i in 0 ..= K - 1
        {
            next[i] = value & (1 << i) != 0;
        }
        Automaton(next)
    }
}

Ziemlich einfach. Hier gibt es nur ein paar Tricks.

1. Wir müssen sowohl das Array als auch die u64 in der gleichen Richtung durchlaufen, d.h. von der niedrigstwertigen Zelle zur höchstwertigen Zelle. Für das Array bedeutet dies, dass wir von Null an aufwärts indizieren; für u64 bedeutet dies, dass wir von²⁰ bis 2⁽⁶³⁾ aufwärts maskieren.
2. Der assert! Makroaufruf ist ein dynamischer Wächter über den Wert des const Parameters K. count_zeros ist ein const fn, den wir verwenden, um die Anzahl der Bits in einem u64 zu erhalten. Wir könnten stattdessen das Literal 64 einfügen, natürlich von , aber diese Technik bewahrt eindeutig die Korrelation zwischen dem Typ und seiner Bitlänge. Da K ein konstanter Parameter ist und count_zeros ein const fn mit einem literalen Empfänger (0u64) ist das gesamte Prädikat ein const Ausdruck, was bedeutet, dass der Compiler die Laufzeitprüfung wegoptimieren kann, wenn der const-Ausdruck zu true ausgewertet wird. Im Freigabemodus ist dieser schließlich doch ein statischer Guard!

ℹ️ Grenzen der Implementierung von Const

Hinweis: Konst-Implementierungsgrenzen, d.h. Konst-Ausdrücke in const-Parameterpositionen, sind in Nightly Rust verfügbar, aber nicht in Stable Rust. Mit der Nightly Toolchain könnten wir eine bedingte Trait-Implementierung auf einem nicht verwandten Hilfstyp verwenden, um statisch vor Werten außerhalb des Bereichs von K zu schützen, indem ein Compilerfehler ausgegeben wird.

// Available in nightly only.
trait IsTrue {}
struct Guard<const C: bool>;
impl IsTrue for Guard<true> {}

impl<const K: usize> From<u64> for Automaton<K> where Guard<{K <= 64}>: IsTrue
{
    fn from(value: u64) -> Self
    {
        // …
    }
}

In diesem Szenario deaktiviert K außerhalb des Bereichs die Implementierung von From für Automaton, so dass der Compiler beim Versuch, from mit z.B. Automaton zu verwenden, meldet, dass die Eigenschaft nicht implementiert ist.

Aber die assert! Technik ist das Beste, was wir mit stabilem Rust tun können, und wir verwenden stabiles Rust in diesem Projekt, um die Stabilität und Verfügbarkeit zu maximieren.

Testen des evolutionären Mechanismus

Bevor wir zu Bevy übergehen, sollten wir testen, ob dies alles funktioniert. Wir wählen eine beliebige Ausgangsgeneration und eine Regel, führen mechanisch eine Evolution von Hand durch und verlassen uns dann auf die strukturelle Induktion, um festzustellen, dass die Implementierung korrekt ist. Da wir frei wählen können, was wir wollen, wählen wir die Anfangsgeneration 0x34244103 und die Regel #110. Außerdem wählen wir der Einfachheit halber einen kürzeren Automaten - 30 Zellen anstelle von 64 - aus. Dieses Szenario ist auf Wikipedia illustriert, so dass wir es als einen von der Community geprüften Testvektor behandeln können.

#[test]
fn rule_110()
{
    //     XX•X••••X••X•••X•••••X••••••XX
    // 0b00110100001001000100000100000011
    // 0x   3   4   2   4   4   1   0   3
    let automaton = Automaton::<30>::from(0x34244103);
    //     •XXX•••XX•XX••XX••••XX•••••XX•
    // 0b00011100011011001100001100000110
    // 0x   1   C   6   C   C   3   0   6
    let expected = Automaton::<30>::from(0x1C6CC306);
    let actual = automaton.next(110.into());
    assert_eq!(expected, actual);
}

Ringpuffer und impl Trait Syntax

Wir wollen jedoch mehr als eine Generation visualisieren, weil wir sonst keine coolen Serien oder Strukturen wie Sierpiński-Dreiecke erleben können. Wir wollen sehen, wie sich ein zellulärer Automat im Laufe der Zeit entwickelt, zumindest im Laufe von, sagen wir, fünfzig Generationen.

pub const AUTOMATON_HISTORY: usize = 50;

Um zu vermeiden, dass zu viel Speicherplatz benötigt wird oder ein scrollbares Ansichtsfenster untergebracht werden muss, haben wir die Entwicklung auf AUTOMATON_HISTORY Generationen beschränkt. Wir sollten natürlich nur die jüngsten Generationen aufbewahren, wobei die aktuelle Generation an der Grenze steht. Ein Ringpuffer scheint die natürliche Wahl zu sein, um diese Ziele zu erreichen.

Die Kiste ringbuffer bietet eine solide Implementierung mit einer praktischen API, die wir in unser Projekt einbinden können. Wir fügen Folgendes zu unserem Cargo.toml:

[dependencies]
ringbuffer = "0.15.0"

Zurück in src/automata.rs führen wir History als einen weiteren const-generic newtype ein, der eine ConstGenericRingBuffer umhüllt:

#[derive(Debug, Resource)]
pub struct History<
    const K: usize = AUTOMATON_LENGTH,
    const N: usize = AUTOMATON_HISTORY
>(
    ConstGenericRingBuffer<Automaton<K>, N>
);

Wie der Name bereits andeutet, verwendet ConstGenericRingBuffer auch die Generizität const und passt damit perfekt zu unserer Strategie. Wenn wir an unsere Benutzeroberfläche denken, müssen wir einen gesamten Verlauf darstellen, vielleicht mit einer einzigen aktiven Generation am Ende. Wir könnten die Logik für die Einrichtung der Benutzeroberfläche als Spezialfall verwenden, aber da der Speicher für den Ringpuffer bereits belegt ist, ist es sauberer, History mit leeren Automaten zu füllen.

impl<const K: usize, const N: usize> History<K, N>
{
    pub fn new() -> Self
    {
        let mut ring = ConstGenericRingBuffer::new();
        for _ in 0 .. N
        {
            ring.push(Automaton::default());
        }
        assert!(ring.is_full());
        Self(ring)
    }
}

ConstGenericRingBuffer::new baut einen leeren Ringpuffer auf und unsere Schleife füllt ihn mit leeren Automaten. Die Fülle des Ringpuffers ist eine wesentliche Voraussetzung für unseren Anwendungsfall, daher haben wir für Aufrichtigkeit. Jetzt können wir durch die Geschichte iterieren, von oldest bis newest, und wissen, dass fünfzig Generationen auftreten werden.

impl<const K: usize, const N: usize> History<K, N>
{
    pub fn newest(&self) -> &Automaton<K> { self.0.back().unwrap() }
    pub fn oldest(&self) -> &Automaton<K> { self.0.front().unwrap() }
    pub fn iter(&self) -> impl Iterator<Item=&Automaton<K>> { self.0.iter() }
}

Wir können unwrap sicher in newest und oldest aufrufen, weil wir für Fülle gesorgt haben, was eine stärkere Voraussetzung ist als die Nicht-Entbehrlichkeit, die alles ist, was unwrap hier verlangt.

Aber das Interessanteste hier ist der Rückgabetyp von iter, der das verwendet, was Rust impl Trait Syntax nennt. Der konkrete Iterator, der in der Kiste definiert ist, heißt und ist für die Kiste privat. Wir können diesen Typ in unserem eigenen Code überhaupt nicht benennen, d.h. wir können ihn weder direkt in einer Methodensignatur erwähnen noch innerhalb eines anderen Typs kapseln. deklariert, dass wir einen konkreten Typ zurückgeben, der den Trait implementiert, aber die Identität dieses Typs bleibt vage. Dadurch bleibt der private Typ sogar für uns verborgen, aber wir können diesen Typ trotzdem anonym aus unserer eigenen API wieder exportieren. Diese Art von Ad-hoc-Generizität ist an API-Grenzen sehr nützlich und ergonomischer als die Einführung eines benannten Typparameters.

Den Automaten weiterentwickeln

Die Entwicklung des zellulären Automaten ist eine einfache Angelegenheit, bei der wir die Daten und die Logik verwenden, die wir bereits gesehen haben:

impl<const K: usize, const N: usize> History<K, N>
{
    pub fn evolve(&mut self, rule: AutomatonRule)
    {
        self.0.push(self.newest().next(rule));
    }
}

Das ist alles, was wir vom Modell brauchen, also ist es an der Zeit, die src/automata.rs hinter sich zu lassen und uns der Benutzeroberfläche zuzuwenden - im nächsten Blogbeitrag dieser Serie.