This article was originally published at 47deg.com on October 01, 2020.
Optics provide a language for data access and manipulation. They fit the functional paradigm very well, because their focus on composability – you build more complex optics from a small set of building blocks – and immutability – whenever you apply an operation to a value, a copy is returned, in constrast with mutable approaches. Libraries like Monocle for Scala, with a port to TypeScript, Arrow Optics for Kotlin, Bow Optics for Swift, Aether for F#, optics and lens for Haskell give an idea of the popularity within these communities.
As a beginner with optics, though, you can be easily overloaded by a dozen terms. Lenses, prisms, (affine) traversals . . . they all seem similar, but different. But this does not have to be the case! Underlying this zoo of optics, there are an orthogonal set of concepts, which, mixed in the right proportion, give rise to the different optics.
In essence, different kinds of optics provide different operations. Any operation always requires at the very least the optic and the data to which it should be applied. One of the simplest is accessing a value within a record, usually called get or view. Different libraries choose its syntax depending on the best style in their respective languages:
data ^. _field -- Haskell + optics
Record.field.get(data) // Kotlin + Arrow Optics
Amount of values
A very important idea in this framework is that, in contrast to usual getter/setter pairs, an optic can target zero, one, or an unrestricted amount of positions within your data.
For example, when we apply a modification using an optic targeting element of an array (unrestricted amount), such operation is applied to every element in bulk. We also have optics that target optional values (think of a key in a JSON document that may be missing). In any of the three cases, modification can be performed in two ways:
settakes a single value, and replaces every position pointed by the data with it. That means that, if you usesetalongside an optic targeting all the elements in a tree, the new copy keeps the same structure, but all nodes now hold the same single value.over/modifytakes a function that is applied at each position targeted by the optic.
Whereas you apply modifications irrespectively from the amount of targets, the access operations must be aware of this fact. For that reason, optics frameworks usually provide three levels of “getters”:
view/gettargets exactly one value, like a property in an object that we are guaranteed to have.preview/getOptionaltargets zero or one values, which essentially amounts to an optional value, like an index in an array that may go out of bounds.reduce/traverseandtoList/toArraytarget an unrestricted amount, like the aforementioned array or the values within an object.
It is always safe to treat an optic in a less restricted way. For example, if your optic targets exactly one value, you can also use preview or toList over it. As we will see in a second, this is important for optics composition.
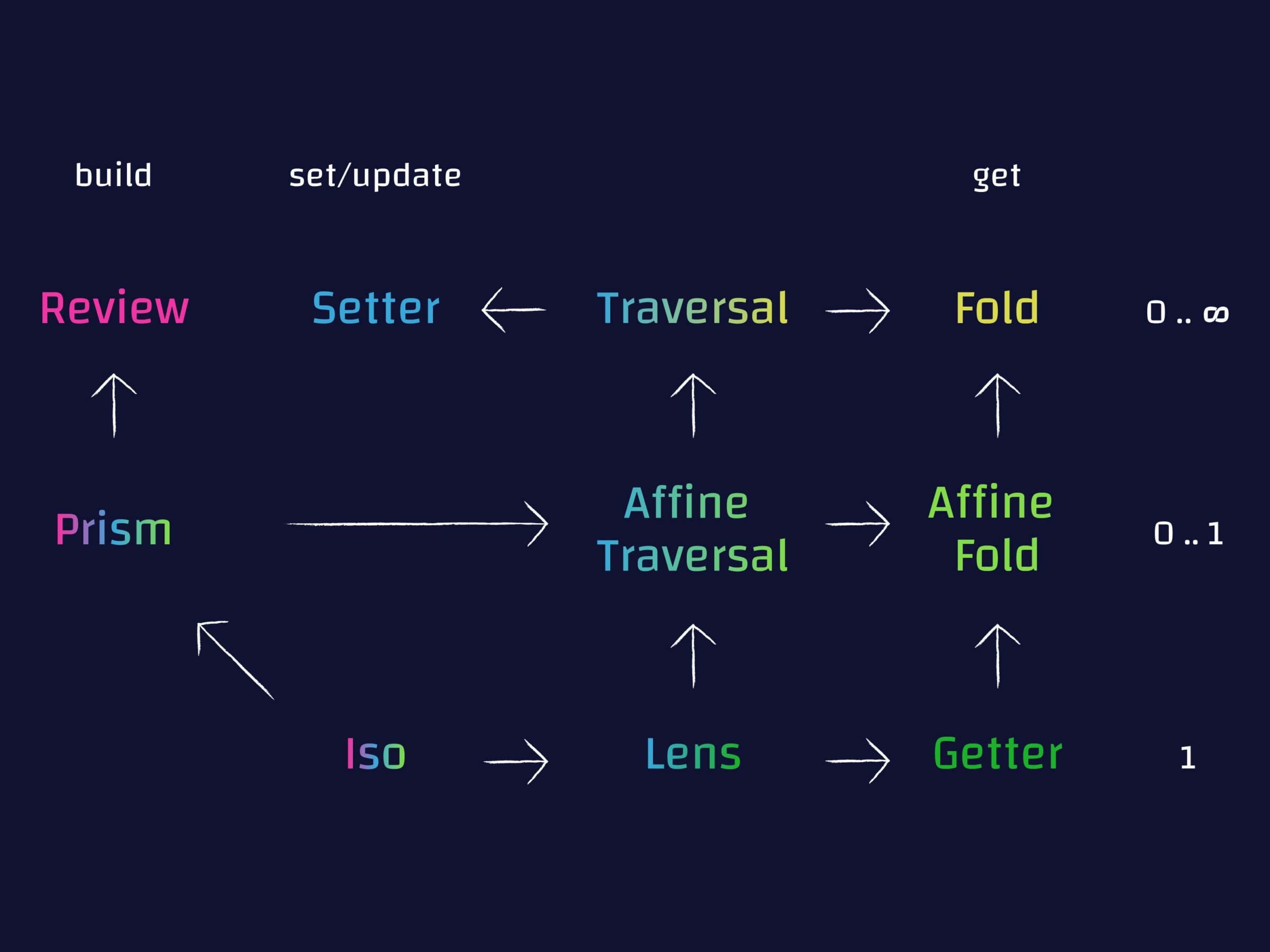
Since we have three “levels of amounts” and two possibilities for setting (we are able or not), we get six different kinds of optics, plus an additional one for setting without access. This is where the zoo of names comes into play: almost every square gets a different name – in some cases, the same square receives different names depending on the library.
set? | Exactly 1 | 0 or 1 | Unrestricted | No access |
|---|---|---|---|---|
| Yes | Lens | Optional/AffineTraversal | Traversal | Setter |
| No | Getter | PartialGetter/AffineFold | Fold | does not exist |
As mentioned above, one of the advantages of optics are their compositionality. You can compose any two optics provided they share some common operation, and the result is the strongest optic that complies with it. Let me unwrap this with an example: say you want to compose an Optional/AffineTraversal (zero or one values, both get and set) with a Getter (exactly one value, only get). The result must be the optic that targets zero or one values (since targeting one value can be downgraded to that case), and only allows getting (since Getter does not provide the setting capability). This means the composition of Optional/AffineTraversal and Getter is a PartialGetter/AffineFold.
Builders
The previous six kinds of optics can only access or modify values. There is one additional capability an optic may have: being able to create values. Take for example a Result type whose Error case holds a single string value. From that single string we can create a whole Result; this means we can build an _Error optic – a prism in this case – which can both get and create.
_Error # "network failed" -- Haskell + optics
Result.Error.reverseGet("network failed") // Kotlin + Arrow Optics
This adds yet another axis to our previous table, depending on whether when accessing you are guaranteed to have a value or not. Following with our example of Result, _Error holds an optional value, because a Result may also be _Success, and, in that case, there is no error value to obtain.
| Exactly 1 | 0 or 1 | Unrestricted | No access |
|---|---|---|---|
Iso | Prism | does not exist | Review / ReverseGet |
Something quite interesting is that, if you can provide a way to get and to build, you are also providing a way to set or modify. For that reason, both Iso and Prism are also in the set/modify part of the hierarchy.
The whole hierarchy
After all this discussion, we have found ten interesting combinations of operations, each one with a different name. The following diagram describes their relations, with an arrow meaning that a certain optic provides more features than its parent, or conversely, that it can be casted into it.
Summary
Optics are becoming increasingly popular in functional programming circles, due to its conciseness and how well it works with immutable data.
If you’re interested in learning more, check out the Optics course that is available in the Xebia Functional Academy.





