Bandit Freitag

Haben Sie jemals Ihren eigenen Bandit-Algorithmus implementiert? Möchten Sie wissen, wie Sie anfangen können? Lesen Sie weiter, um herauszufinden, wie Sie einfache kontextbezogene Bandits von Grund auf erstellen können, inklusive Code.

Dieser Blog ist das Ergebnis eines Freitags-Hackathons (das erklärt den Titel), bei dem einige Kollegen und ich kontextuelle Banditen erforschen wollten. Unser Ziel war es, die einfachste Version eines kontextuellen Banditen zu bauen, die uns einfiel.

Gliederung

• Was ist ein (kontextueller) Bandit?
• Was ist der praktische Anwendungsfall?
• Wie sieht die Aufstellung aus?
• Wie können wir unsere Banditen testen?
• Wer ist der Gewinner?
• Das war's dann wohl

Mehrarmiger Bandit

Das Problem des mehrarmigen Banditen hat seinen Ursprung in dem hypothetischen Experiment, den besten Arm an einem Spielautomaten zu wählen. Da man nicht weiß, welcher Arm die beste Belohnung bringt, versucht man, dies experimentell herauszufinden, indem man nach dem Zufallsprinzip die Arme zieht und weiterhin die Arme mit den höchsten Belohnungen zieht (ausnutzt).

Kontextueller Bandit

Ein kontextabhängiger Bandit ist ein Bandit-Algorithmus, bei dem die Belohnung vom Kontext (auch Umgebung genannt) abhängt. Nehmen wir zum Beispiel an, dass die Auszahlung an einem Spielautomaten vom Alter der Person abhängt, die den Arm zieht. Dann wollen wir für jedes Alter (oder jede Altersgruppe) den Arm mit der höchsten Belohnung herausfinden. Bei einem fairen Spielautomaten sollte der Kontext natürlich keinen Einfluss auf das Ergebnis haben, aber in praktischen Anwendungen, bei denen Bandit-Algorithmen zum Einsatz kommen, hat der Kontext oft einen Einfluss.

Je mehr Kontexte Sie jedoch berücksichtigen, desto mehr Zeit benötigen Sie, um die optimale Aktion für jeden Kontext zu lernen.

Was ist der praktische Anwendungsfall?

Die Anwendung, die uns vorschwebte, war die Empfehlung von Produkten für Kunden. Übertragen auf Spielautomaten bedeutet dies, dass jedes Produkt ein Arm am Spielautomaten ist. Wir nehmen an, dass die Kauf-/Klickwahrscheinlichkeit für jeden Kunden für jedes Produkt sowohl vom Alter als auch vom Vermögen abhängt (dies ist der Kontext, den der kontextuelle Bandit lernen sollte). Wiederum im Kontext von Spielautomaten bedeutet dies, dass Alter und Vermögen der Person, die den Arm zieht, die Belohnung beeinflussen.

Eine solche Empfehlungseinstellung hat viele reale Anwendungen, wie die Empfehlung von Produkten auf E-Commerce-Websites wie Bol.com und Amazon. Auch die Empfehlung von Inhalten auf z.B. Netflix oder Werbung durch Google sind sehr ähnlich.

Wie sieht die Aufstellung aus?

Baseline Bandit

Der Basis-Bandit lernt aus historischen Daten die gesamte Klick-/Kaufrate pro Produkt. Er empfiehlt immer das Produkt mit der höchsten Klick-/Kaufrate und lernt daher nach der anfänglichen Trainingsphase nicht mehr dazu.

Thompson Stichprobenbandit

Das Thompson Sampling, benannt nach William R. Thompson, ist eine Heuristik für die Auswahl von Aktionen, die das Erkundungs-Ausbeutungs-Dilemma im mehrarmigen Banditenproblem angeht. Sie besteht darin, die Aktion zu wählen, die die erwartete Belohnung in Bezug auf eine zufällig gezogene Überzeugung maximiert.

Der auf dem Thompson-Sampling basierende Bandit (siehe Wikipedia-Definition oben) funktioniert wie folgt. Für jedes Produkt wird eine Kauf-/Klickwahrscheinlichkeit auf der Grundlage der Beta-Verteilung aus den historischen Daten ermittelt und das beste Produkt entsprechend ausgewählt. Nach jeder Empfehlung werden die Wahrscheinlichkeiten aktualisiert. Dadurch lernt dieser Bandit ständig dazu, da selbst Produkte mit geringer Kauf-/Klickwahrscheinlichkeit eine Chance haben, ausgewählt zu werden.

Kontextueller Bandit

Unser kontextbezogener Bandit ist eigentlich ein Wrapper-Bandit, da er Alter und Wohlstand in Gruppen einteilt und einen Bandit der Wahl auf jede Gruppe anwendet. Das heißt, das Problem wird in viele Unterprobleme aufgeteilt, die unabhängig voneinander gelöst werden.

Die Anzahl der zu verwendenden Bins ist ein Kompromiss zwischen der Flexibilität beim Lernen und der Datenmenge, die Ihnen zur Verfügung steht (bzw. der Zeit, die Sie benötigen, um sie zu sammeln). Es ist ein Parameter, aus dem gleich breite Bins erstellt werden.

Betrügerischer Bandit

Um zu sehen, wie weit wir von der optimalen Leistung entfernt sind, haben wir einen betrügerischen Banditen erstellt, der die für die Datengenerierung verwendeten Wahrscheinlichkeiten verwendet, um zu ermitteln, welche Produkte in einem bestimmten Kontext die höchste Klick-/Kaufrate haben werden. Nur mit Glück können Sie eine bessere Leistung erzielen.

Wie können wir unsere Banditen testen?

Um die Qualität der Bandit-Algorithmen, die wir erstellen werden, zu überprüfen, müssen wir das System definieren, das die Belohnung für jede Aktion in jedem Kontext bestimmt. Die Verwendung vorhandener Datensätze gibt uns wenig Kontrolle. Daher haben wir uns entschieden, Daten zu generieren, mit denen wir eine Vielzahl verschiedener Produkte mit unterschiedlichen Belohnungen und unterschiedlichen Auswirkungen des Kontexts erstellen können.

Prozess der Datengenerierung

Für jedes Produkt wählen wir eine bestimmte Verteilung (wir verwenden wild variierende Formen), die die erwartete Belohnung für jeden Kontext bestimmt. Bei Kartoffeln z.B. ist die Klick-/Kaufwahrscheinlichkeit max(0, Alter - Wohlstand^2).

Aus diesen Verteilungen können wir dann Trainingsdaten entnehmen. Und nach dem Training können wir so viele Testdatensätze nehmen, wie wir wollen, um die Leistung jedes Banditen fair zu bestimmen.

Dies sind die Schritte, um einen einzelnen Datensatz zu prüfen:

1. Zufällige Auswahl des Kontextes für einen Kunden: Alter und Vermögen (der Einfachheit halber beide zwischen 0 und 1)
2. aus der für jedes Produkt definierten Verteilung eine Stichprobe des Kauf-/Klickverhaltens (Richtig oder Falsch) auf der Grundlage des Stichprobenkontexts aus Schritt 1.

Beispielhafte Daten

Nachfolgend ein Beispiel für die generierten Daten. Jeder Datensatz stellt dar, wie ein Kunde mit einem bestimmten Kontext (Alter und Vermögen) auf jedes der Produkte reagieren würde, d.h. ob er kaufen/klicken würde.

Zum Beispiel werden für den ersten Datensatz zunächst das Alter und das Vermögen zufällig zwischen 0 und 1 auf 0,82 bzw. 0,33 gesetzt. Dann schauen wir uns für jedes Produkt die gewählten bedingten Wahrscheinlichkeiten an, um für die Kauf-/Klickaktion Wahr oder Falsch zu wählen. Für Kartoffeln beträgt die bedingte Wahrscheinlichkeit für das gegebene Alter und Vermögen 0,82-0,33^2 = 0,71. Wir wählen also Wahr mit einer Wahrscheinlichkeit von 0,71 und Falsch mit einer Wahrscheinlichkeit von 0,29.

Prozess der Datenerzeugung visualisiert

Unten sehen Sie eine Visualisierung der gewählten bedingten Kaufwahrscheinlichkeiten für jedes unserer Produkte auf der Grundlage von Alter und Vermögen.

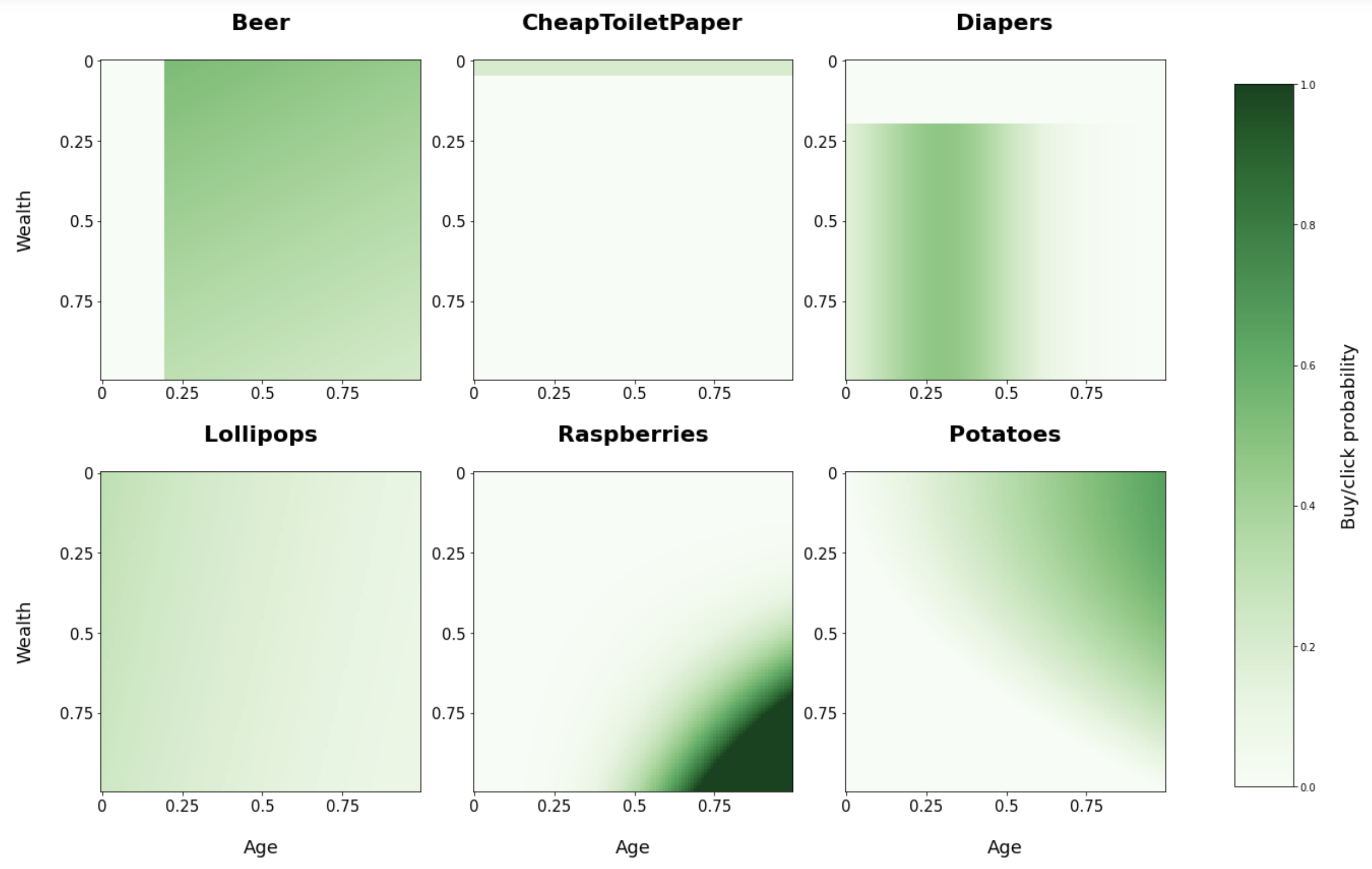
Aus diesen Diagrammen können Sie zum Beispiel ersehen, dass Himbeeren eher von alten und wohlhabenden Menschen gekauft werden. Und billiges Toilettenpapier nur mit einer geringen Wahrscheinlichkeit von sehr armen Menschen und überhaupt nicht von den übrigen.

Wer ist der Gewinner?

Wir haben einen Simulator entwickelt, um die verschiedenen Banditen zu bewerten. Jeder Bandit hat die Option, mit einigen historischen Daten (1.000 Datensätze) zu trainieren. Außerdem kann jeder Bandit entweder Vanilla oder die kontextbezogene Variante mit Binning sein. Unten sehen Sie die Ergebnisse (sortiert nach Leistung) für 10.000 Empfehlungen.

Bandit	Ausbildung	Kontextbezogen	Kaufen/Klicken (%)
Schummeln	-	-	49.91
Basislinie	Ja	Ja	42.53
Thompson-Probenahme	Ja	Ja	42.14
Thompson-Probenahme	Nein	Ja	40.26
Basislinie	Nein	Ja	30.45
Basislinie	Ja	Nein	30.68
Basislinie	Nein	Nein	29.55
Thompson-Probenahme	Ja	Nein	30.29
Thompson-Probenahme	Nein	Nein	28.79

Beobachtungen

• Wie erwartet übertreffen die kontextuellen Banditen die Vanille-Banditen bei weitem.
• Die Baseline benötigt Trainingsdaten, um eine gute Leistung zu erbringen, da sie nicht erforscht, ohne Trainingsdaten ist sie nur eine zufällige Schätzung.
• Ohne Trainingsdaten hatte die Baseline das Glück, dass sie zufällig ein Produkt mit einer hohen Gesamtumsatzrate auswählte.
• Es ist überraschend, dass die kontextbezogene Basislinie mit Training den kontextbezogenen Thompson Sampling Bandit übertrifft, da es sich um einen so einfachen Algorithmus handelt.
• Der Thompson Sampling Bandit wird wahrscheinlich besser verallgemeinern als die Basislösung, z. B. wenn es nicht nur ein einziges Produkt gibt, das in jedem Kontext sehr beliebt ist. Oder wenn sich die Wahrscheinlichkeiten im Laufe der Zeit ändern, ist er in der Lage zu lernen und sich nach der Initialisierung anzupassen.

Taugen diese Banditen etwas?

Betrachtet man die Leistung des betrügerischen Banditen (fast 50 %), scheint eine Umwandlung von 43 % für den Zweitplatzierten ziemlich gut zu sein. Vor allem, wenn man bedenkt, wie einfach diese Banditen sind. Sie können in nur wenigen Zeilen Code implementiert werden.

Das war's dann wohl

Wir haben einige einfache Bandit-Algorithmen erstellt und kontextabhängige Variationen davon entwickelt. Anhand einiger generierter Daten sind wir zu dem Schluss gekommen, dass diese einfachen Algorithmen recht anständig funktionieren.

Arbeiten Sie an einem Empfehlungsproblem und erwägen Sie den Einsatz von Banditen? Ich wäre an Ihren Erfahrungen interessiert. Viel Spaß beim Codieren!